A(2;2) , B(6;6)
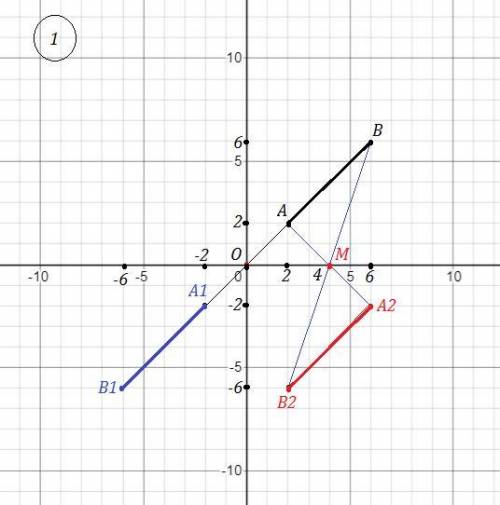
1) Чтобы начертить отрезок, симметричный отрезку АВ относительно точки О(0;0) , надо соединить точку О с точками А и В и отложить от точки О отрезки, равные ОА и ОВ . Получим отрезок А1В1 . Рис. 1 .
А1(-2;-2) , В1(-6;-6)
2) 1) Чтобы начертить отрезок, симметричный отрезку АВ относительно точки М(4;0) , надо соединить точку М с точками А и В и отложить от точки М отрезки, равные МА и МВ . Получим отрезок А1В1 . Рис. 1 .
А2(6;-2) , В2(2:-6)
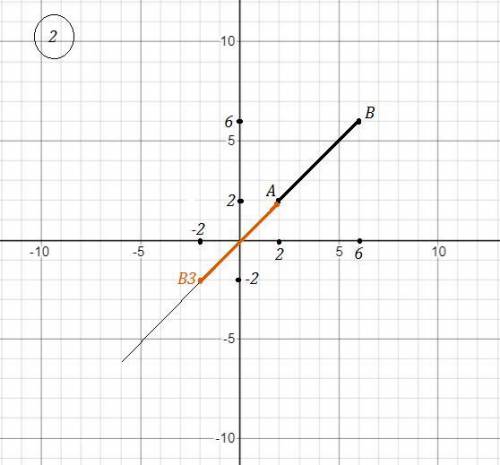
3) 1) Чтобы начертить отрезок, симметричный отрезку АВ относительно точки А(2;2) , надо продлить отрезок АВ и от точки А отложить отрезок, равный отрезку АВ . Получим отрезок АВ3 . Рис. 2.
А(2;2) , В3(-2;-2)
1) 1 случай a=0, то уравнение примет вид: (n+1)x + 1=0
x=-1/(n+1), отсюда видно, что n-любое действительное число, кроме n= -1( ибо в знаменателе будет ноль)
2) 2 случай a неравно 0
тогда имеем: ax^2+(n+1)x +1=0, чтобы уравнение имело имело решения дистриминант должен быть больше или равнятся нулю.
D=(n+1)^2 -4a>или равно нулю
(n+1)^2> или = 4а
отсюда видно, что число в квадрате всегда будет больше или равно нулю, если а будет больше или равно нулю
Значит n-любое, если а>или=0
ответ: 1) n- любое , кроме n=-1. 2) n- любое, если а> или=0( вот тут совнемаюсь немного)
3x-2y=-1 3x-2*(4x²-2)=-1
3x-8x²+4+1=0
-8x²+3x+5=0, D=3²-4*(-8)*5=169
x₁=1, x₂=-5/8
{x₁=1 {x₂=-5/8
y₁=2 y₂=17/4
x²+4x-12>5x, x²+4x-5x-12>0
x²-x-12>0 метод интервалов:
x²-x-12=0, x₁=-3, x₂=4
+ - +
||>x
-3 4
x∈(-∞;-3)U(4;∞)