a = 3
Объяснение:
Имеем выражение:
a^2 - 6 * a + 11.
Необходимо найти значение аргумента a, при котором значение выражения будет минимальным.
Здесь можно приравнивать значение выражения к нулю, можно решать квадратное уравнение, можно искать значение переменной методом подбора, но единственный практичный выделить у выражения квадрат суммы или разности двух чисел:
a^2 - 6 * a + 11 = a^2 - 2 * 3 * a + 3 * 3 + 2 = (a - 3)^2 + 2.
Получили сумму квадрата числа и двойки. Наименьшее значение суммы - 2, значит, a = 3.
Введем векторы АВ, BС и АС:
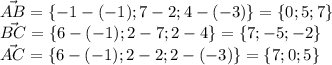
Найдем длины всех сторон треугольника:
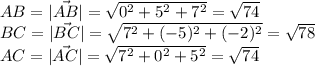
Стороны AB и AC равны, поэтому треугольник - равнобедренный
Учитывая, что треугольник равнобедренный, тупым углом между оказаться только угол, противолежалий основанию, то есть угол А.
Рассмотрим скалярное произведение векторов АВ и АС. С одной стороны скалярное произведение векторов равно сумме попарных произведений их координат:

С другой стороны, скалярное произведение векторов равно произведению их модулей на косинус угла между ними:
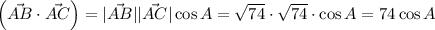
Приравняв два выражения, можно получить значение для косинуса угла между векторами:
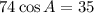
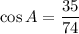
Так как косинус угла А положителен, то угол А острый.
Два других угла В и С не могут быть тупыми, так как они равны, а в треугольнке не можут быть более одного тупого угла.
ответ: треугольник равнобедренный, остроугольный
15+
2) 2636*(