Пусть вкладчик положил 
рублей в банк. Через год вкладчик получит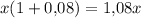 
рублей. После того, как снял деньги, у него остается 
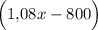рублей. Известно, что на счёте осталась сумма, равная половине первоначального вклада. Составим уравнение
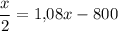
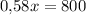
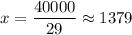
В конце второго года хранения вкладчик получит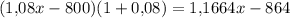 
рублей. Подставив значение х, получим 
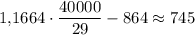рублей.
ответ: на счету у вкладчика в конце второго года хранения будет 745 рублей.
Объяснение:
1) sin2x + cosx = 0.
2) Рассмотрим уравнение по частям.
3) sin2x. Преобразуем по тригонометрической формуле (формула двойного угла). Получаем: sin2x = 2 * sinx * cosx.
4) Подставим полученное значение в уравнение. Получаем: 2 * sinx * cosx + cosx = 0.
5) Преобразуем, с вынесения общего множителя за скобки. Получаем: cosx (2 * sinx - 1) = 0.
6) Произведение равно 0 тогда и только тогда когда хотя бы один из множителей равен 0. Получаем: cosx = 0 или 2 * sinx - 1 = 0.
7) cosx = 0; x = 90
8) sinx = 1/2; x = 30.
ответ: поставим заданное решение в первое уравнение системы - 9/5=(7/5-5)/(2*а)=-3,6/(2*а) или -18=-18*а или а=1. Проверим второе уравнение - 9/5=(0,2*(4-5*1)-7)/(4*1)=-1,8=-9/5 верно!
ответ при а=1.
Объяснение: