Алгебра: Сократите дробь 9x^2-6x+1/3x^2-7x+2

Сократите дробь 9x^2-6x+1/3x^2-7x+2

👇

Ответ:

entogenes

02.05.2022

В числителе полный квадрат: (3x - 1)^2
для знаменателя D=49-4*3*2 = 5^2
корни (7 +- 5)/6
3x^2 - 7x + 2 = 3(x - 2)(x - 1/3) = (x - 2)(3x - 1)
ответ: (3х - 1) / (х - 2)

4,6(33 оценок)

Открыть все ответы

Ответ:

romanowacristi

02.05.2022

Объяснение:

Первая система линейных уравнений:

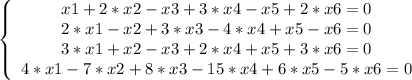
$\left \{ \begin {array}{cccc} x1+2*x2-x3+3*x4-x5+2*x6=0 \\ 2*x1-x2+3*x3-4*x4+x5-x6=0 \\ 3*x1+x2-x3+2*x4+x5+3*x6=0 \\ 4*x1-7*x2+8*x3-15*x4+6*x5-5*x6=0 \end{array}\right$

1-ое уравнение умножаем на -2 и складываем со 2-ым уравнением.

1-ое уравнение умножаем на -3 и складываем с 3-им уравнением.

1-ое уравнение умножаем на -4 и складываем с 4-ым уравнением.

Получаем нули при x1 во всех уравнениях, кроме 1-го:

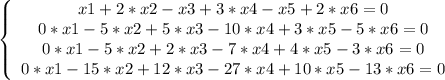
$\left \{ \begin {array}{cccc} x1+2*x2-x3+3*x4-x5+2*x6=0 \\ 0*x1-5*x2+5*x3-10*x4+3*x5-5*x6=0 \\ 0*x1-5*x2+2*x3-7*x4+4*x5-3*x6=0 \\ 0*x1-15*x2+12*x3-27*x4+10*x5-13*x6=0 \end{array}\right$

2-ое уравнение умножаем на -1 и складываем с 3-им уравнением.

2-ое уравнение умножаем на -3 и складываем с 4-ым уравнением.

Получаем нули при x2 во всех уравнениях, кроме 1-го и 2-го:

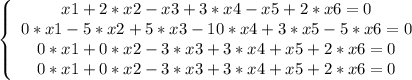
$\left \{ \begin {array}{cccc} x1+2*x2-x3+3*x4-x5+2*x6=0 \\ 0*x1-5*x2+5*x3-10*x4+3*x5-5*x6=0 \\ 0*x1+0*x2-3*x3+3*x4+x5+2*x6=0 \\ 0*x1+0*x2-3*x3+3*x4+x5+2*x6=0 \end{array}\right$

3-ье и 4-ое уравнения получились одинаковыми, 4-ое отбрасываем:

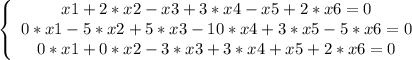
$\left \{ \begin {array}{ccc} x1+2*x2-x3+3*x4-x5+2*x6=0 \\ 0*x1-5*x2+5*x3-10*x4+3*x5-5*x6=0 \\ 0*x1+0*x2-3*x3+3*x4+x5+2*x6=0\end{array}\right$

Получилась система, из которой можно получить фундаментальное решение:

x4, x5, x6 ∈ R

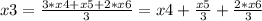
$x3=\frac{3*x4+x5+2*x6}{3}=x4+\frac{x5}{3}+\frac{2*x6}{3}$

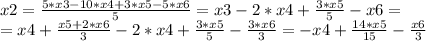
$x2=\frac{5*x3-10*x4+3*x5-5*x6}{5} =x3-2*x4+\frac{3*x5}{5} -x6=\\ =x4+\frac{x5+2*x6}{3} -2*x4+\frac{3*x5}{5} -\frac{3*x6}{3}=-x4+\frac{14*x5}{15}-\frac{x6}{3}$

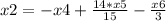
$x2=-x4+\frac{14*x5}{15}-\frac{x6}{3}$

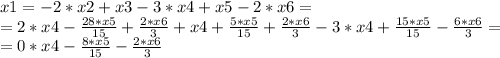
$x1=-2*x2+x3-3*x4+x5-2*x6=\\ =2*x4-\frac{28*x5}{15}+\frac{2*x6}{3} +x4+\frac{5*x5}{15}+\frac{2*x6}{3} -3*x4+\frac{15*x5}{15}-\frac{6*x6}{3} =\\ =0*x4 -\frac{8*x5}{15}-\frac{2*x6}{3}$

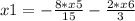
$x1=-\frac{8*x5}{15}-\frac{2*x6}{3}$

Вторая система решается точно также.

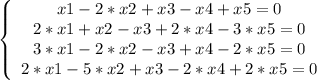
$\left \{ \begin{array}{cccc} x1-2*x2+x3-x4+x5=0 \\ 2*x1+x2-x3+2*x4-3*x5=0 \\ 3*x1-2*x2-x3+x4-2*x5=0 \\ 2*x1-5*x2+x3-2*x4+2*x5=0 \end{array}\right.$

1-ое уравнение умножаем на -2 и складываем со 2-ым уравнением.

1-ое уравнение умножаем на -3 и складываем с 3-им уравнением.

1-ое уравнение умножаем на -2 и складываем с 4-ым уравнением.

Получаем нули при x1 во всех уравнениях, кроме 1-го:

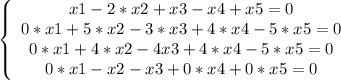
$\left \{ \begin{array}{cccc} x1-2*x2+x3-x4+x5=0 \\ 0*x1+5*x2-3*x3+4*x4-5*x5=0 \\ 0*x1+4*x2-4x3+4*x4-5*x5=0 \\ 0*x1-x2-x3+0*x4+0*x5=0 \end{array}\right.$

4-ое уравнение ставим 2-ым, от этого система не меняется:

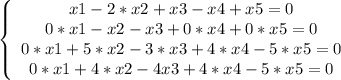
$\left \{ \begin{array}{cccc} x1-2*x2+x3-x4+x5=0 \\ 0*x1-x2-x3+0*x4+0*x5=0 \\ 0*x1+5*x2-3*x3+4*x4-5*x5=0 \\ 0*x1+4*x2-4x3+4*x4-5*x5=0 \end{array}\right.$

2-ое уравнение умножаем на 5 и складываем с 3-им уравнением.

2-ое уравнение умножаем на 4 и складываем с 4-ым уравнением.

Получаем нули при x2 во всех уравнениях, кроме 1-го и 2-го:

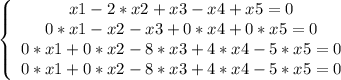
$\left \{ \begin{array}{cccc} x1-2*x2+x3-x4+x5=0 \\ 0*x1-x2-x3+0*x4+0*x5=0 \\ 0*x1+0*x2-8*x3+4*x4-5*x5=0 \\ 0*x1+0*x2-8*x3+4*x4-5*x5=0 \end{array}\right.$

3-ье и 4-ое уравнения получились одинаковыми, 4-ое отбрасываем:

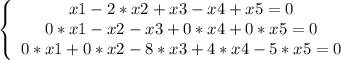
$\left \{ \begin{array}{ccc} x1-2*x2+x3-x4+x5=0 \\ 0*x1-x2-x3+0*x4+0*x5=0 \\ 0*x1+0*x2-8*x3+4*x4-5*x5=0 \end{array}\right.$

Получилась система, из которой можно получить фундаментальное решение:

x4, x5 ∈ R

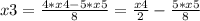
$x3=\frac{4*x4-5*x5}{8}=\frac{x4}{2} -\frac{5*x5}{8}$

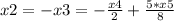
$x2=-x3=-\frac{x4}{2}+\frac{5*x5}{8}$

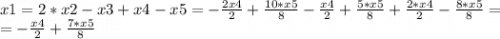
$x1=2*x2-x3+x4-x5=-\frac{2x4}{2}+\frac{10*x5}{8} -\frac{x4}{2}+\frac{5*x5}{8} +\frac{2*x4}{2}-\frac{8*x5}{8} =\\ =-\frac{x4}{2}+\frac{7*x5}{8}$

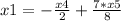
$x1=-\frac{x4}{2}+\frac{7*x5}{8}$

4,6(52 оценок)

Ответ:

slia1984

02.05.2022

Решение
Графиком функции является парабола, ветви которой направлены вверх. 1)      D (f) =R , т.к. f – многочлен. 2)       f(-х) = (-х)2 - 4(-х) - 5 = х2 + 4х – 5   Функция поменяла знак частично, значит, f не является ни чётной, ни нечётной. 3)      Нули функции: При х = 0     у = - 5; (0;-5)  при у = 0      х2 - 4х – 5 = 0 По теореме, обратной теореме Виета х1 = -1; х2 = 5 (-1;0); (5;0). 4)      Найдём производную функции f: f ′(х) = 2х – 4 Найдём критические точки: f ′(х) = 0; 2х – 4 = 0; х = 2 – критическая точка
                f ′(х)                      -                                           + f (х)                                                                                                2                                                            х
                                                   min               5) Найдём промежутки монотонности: Если функция возрастает, то   f ′(х) > 0 ; 2х – 4 > 0; х > 2. Значит, на промежутке (2; ∞) функция возрастает. Если функция убывает, то     f ′(х) < 0; 2х – 4 < 0; х < 2. Значит, на промежутке (- ∞; 2) функция убывает. 6)      Найдём координаты вершины параболы: Х =Y = 22 - 4*2 – 5 = -9 (2;-9) – координаты вершины параболы.
7) Область изменения функции Е (у) = (-9; ∞)   8)      Построим график функции:
                             у
                                                   -1       2       5                                                    -5                                                х

4,4(81 оценок)

Это интересно:

Дом-и-сад

17.04.2023

Как правильно покрасить древесину: советы от профессионалов...

Путешествия

23.02.2023

Как развить туристический бизнес: советы от экспертов...

Образование-и-коммуникации

21.01.2020

10 способов усовершенствовать свой этикет в электронной почте...

Питомцы-и-животные