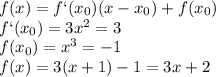
вначале нужно раскрыть скобки. напоминаю, что если перед скобкой стоит член, то нужно каждый член в скобках перемножить на член, стоящий перед скобкой, при чем сами скобки уберутся.
чтобы умножить скобку на скобку, нужно каждый член из первой скобки перемножить на каждый член из второй скобки.
также здесь есть формулы сокращенного умножения.
D= в²-4ас.
поехали))
1. 4х²-4х+1= 6-3х²+12
7х²-4х-17=0
D=16+476=272
х1= 4-4√17\2= 4(1-√17)\2= 2-2√17
х2= 4+4√17\2= 4(1+√17)\2= 2+2√17
ответ: 2-2√17, 2+2√17
2. х²-х-2х+2= х²-7х+6х-42
-2х-44=0
2х=-44
х= - 22
ответ: -22
3. у²+у+2у+2= у²+2у-3у-6
-2у=-8
2у=8
у=4
ответ: 4
4. 4х²+12х+9-(х²-4х+4)-5=0
4х²+12х+9-х²+4х-4-5=0
3х²+16х=0
х(3х+16)=0
х=0 или 3х= -16
х= -16\3
ответ: 0, -16\3
5. 15х+25-9х²-15х-2х²+6х-25=0
7х²+6х=0
х(7х+6)=0
х=0 или 7х= -6
х= -6\7
ответ: 0, -6\7
пусть f(n) - наибольшее значение функции, это означает, что
f(n)>f(n+1)
и
f(n)>f(n-1)
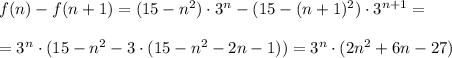
3^{n} >0 при любом n>1
2n²+6n-27 > 0
D=36-4·2·(-27)=252
n > (-6+√252)/4, n - натуральное и не принимает отрицательных значений
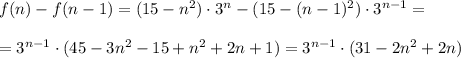
3^{n-1} >0 при любом n >2
-2n²+2n+31 > 0
2n²-2n-31 <0
D=4-4·2·(-31)=252
n < (2+√252)/4
(-6+√252)/4 < n < (2+√252)/4⇒
(-6+√252)/4≈2,5
(2+√252)/4≈4,5
n=3 или n=4
при n=3
f(3)=(15-9)·3³=162
при n=4
f(4)=(15-16)·3⁴=81
О т в е т. 162
Пусть
f(x)=(15-x²)·3ˣ
f`(x)=-2x·3ˣ+(15-x²)·3ˣ·ln3
f`(x)=3ˣ·(-2x+15ln3-x^2ln3)
f`(x)=0
x^2ln3+2x-15ln3=0
D=4-4·ln3·(-15ln3)=4+64ln3
x_(1)≈ x_(2)≈