ответ: (-8; 4).
Объяснение:
Система неравенств:
7(3x + 2) - 3(7x + 2) > 2x;
(x - 5)*(x + 8) < 0.
1. Решим первое неравенство системы. Раскроем скобки:
7(3x + 2) - 3(7x + 2) > 2x;
21х + 14 - 21х - 6 > 2x;
8 > 2x;
2х < 8;
х < 8/2;
х < 4.
2. Решим второе неравенство системы. Чтобы произведение было меньше 0, нужно чтобы один из множителей был меньше нуля:
х - 5 < 0 ⇒ х < 5;
х + 8 < 0 ⇒ х < -8.
3. Оба решения двух неравенств системы, данной по условию, пересекаются на множестве чисел от -8 до 4, тогда ответ будет (-8; 4). Так как неравенства, данные по условию, строгие, что числа -8 и 4 не входят в множество решений.
1) 
, 
, 
.
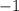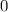2) , 
.
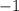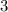Объяснение:
1) По утверждению, обратному лемме Ферма, в точке экстремума функции значение её производной равно нулю. Отсюда следует, что для нахождения точки экстремума функции следует сначала найти производную функции, а затем найти точки, в которых она равна нулю. Они и будут являться точками экстремума исходной функции.
Для данной функции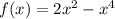 
найдём производную:
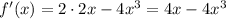. (применены правила: 
, 
)
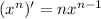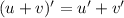Решим теперь уравнение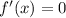 
:
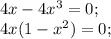
Отсюда следует, что или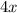 
равно нулю, или 
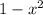равно нулю.
Первое:
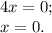
Второе:
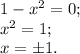
Получается, что точками экстремума функции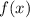 
являются 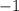, 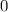и .
2) Аналогично первому заданию, для данной функции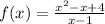 
найдём производную:
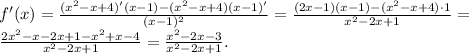(применены правила: , 
, 
, , 
)
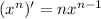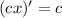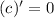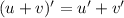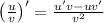Решим теперь уравнение :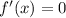
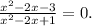
Из него следует, что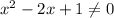 
, а также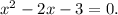 
Для первого:
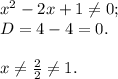
Для второго:
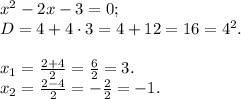
Все 
удовлетворяют условию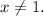 
Получается, что точками экстремума функции 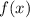являются 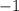и .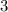
