1) x∈(1;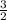 
)
2) x∈(-∞; -3)∪(1; +∞)
Объяснение первого неравенства:
Чтобы произведение было меньше нуля, множители должны иметь разные знаки. Тогда получаем две системы (знака системы сайт не имеет, строчки должны быть объединены фигурной скобкой).
Первая:
x-1<0
2x-3>0
Вторая:
x-1>0
2x-3<0
Решение первой:
x-1<0
x<1;
2x-3>0
2x>3
x>;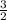
Поскольку мы решали систему, нужно найти пересечение решений. Здесь пересечение - пустое множество, потому что 3/2 больше 1.
Решение второй:
x-1>0
x>1;
2x-3<0
2x<3
x<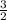
Пересечение решений - x∈(1; 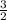) (скобки ставим круглые, потому что знак неравенства строгий)
Объяснение второго неравенства:
Чтобы произведение было больше нуля, множители должны иметь один знак. Тогда получаем две системы:
Первая:
x+3>0
x-1>0
Вторая:
x+3<0
x-1<0
Решение первой:
x+3>0
x>-3;
x-1>0
x>1;
Пересечение: x∈(1; +∞)
Решение второй:
x+3<0
x<-3;
x-1<0
x<1;
Пересечение: x∈(-∞; -3)
Пересекаем решения первой и второй систем и получаем: x∈(-∞; -3)∪(1; +∞)
В решении.
Объяснение:
Великий русский учёный М. В. Ломоносов был первым в стране человеком, который освоил технику мозаичного набора, создавая в собственной мастерской смальту самых разных оттенков. Математик Иванов после посещения Эрмитажа подсчитал, что общая площадь синих и тёмно-серых цветов в панно «Портрет графа Шувалова» составляет 1/4 от всей площади, а примерное их соотношение — 3:57. Размеры этой работы — 46×60 см.
Какова примерная площадь тёмно-серых кусочков на этом панно?
1) Найти площадь панно:
46 * 60 = 2760 (см²);
2) Найти общую площадь синих и тёмно-серых цветов в панно:
2760 * 1/4 = 690 (см²);
3) Эта площадь составляет частей:
3 + 57 = 60;
4) Найти примерную площадь тёмно-серых кусочков на панно:
690 : 60 * 57 = 655,5 (см²).
ответ: 4