![\left[\begin{array}{ccc}-1&2&1\\-1&a&0\\a&2&1\end{array}\right]=\left[\begin{array}{ccc}-1&2&1\\-1&a&0\\a+1&0&0\end{array}\right]](/tpl/images/0065/4734/ed151.png)
Это из третьей строки вычли первую строку. Дальше вычтем из 1 строки вторую, получим матрицу вида
![\left[\begin{array}{ccc}0&2-a&1\\-1&a&0\\a+1&0&0\end{array}\right]](/tpl/images/0065/4734/45cb7.png)
Матрица получилась нижнетреугольная. Ранг матрицы равено количеству линейнонезависимых строк или столбцов в матрице.
Рассмотрим при каких а в матрице появляются нулевые строки
1. а+1=0, а=-1, в этом случаем третья строка зануляется и можно занулить второй столбец. Вычеркиваем нулевую строку и столбец, получаем диагональную матрицу размером 2х2. Количество линейнонезависимых строк=2 значит Rg(A)=2
2. a=0. Получается матрица вида
![\left[\begin{array}{ccc}0&2&1\\-1&0&0\\1&0&0\end{array}\right]](/tpl/images/0065/4734/336ca.png)
Видно, что вторая и третья строки линейно зависимы (2 получается из третьей домножением на -1). Действуя так же как и в случае 1, получаем матрицу 2х2 с линейнонезависимыми строками, значит Rg(A)=2
Во всех остальных случаев ранг матрицы получается равен Rg(A)=3.
Т.к при любых других значениях а матрица имеет диагональный вид. Значит количество линейнонезависимых векторов будет равно 3.
ответ: a=-1 и a=0 Rg(A)=2 ,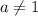 
и ф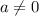
Rg(A)=3
1)
4х^2-х=0
х(4х-1)=0
х=0
4х-1=0
4х=1
х=0,25
ответ. х=0 и х=0,25
2)
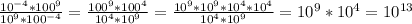
3)
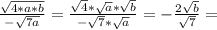
4) один карандаш стоит 1руб 44 коп
5)
5х^2-3х-8<0
5x^2-3x-8=0
(x-1.6)(x+1)=0
Отмечаем корни на оси и находим знаки.
Решением является -1<x<1.6
6)выразим А1 через А2: 6-d и подставим в формулу суммы. Из нее найдем d:
d=11 - разность этой прогрессии,
6-11=-5 - первый член прогрессии.
ответ.А1=-5, d=11
7)
(х-6)(х+3)^3=(х+3)(х-6)^3
сократим на выражение (х-6)(х+3):
(х+3)^2=(х-6)^2
x^2+6x+9=x^2-12x+36
6x+12x=36-9
18x=27
x=1.5
ответ. х=1,5
ответ : -1