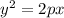 ее фокус находится в точке с координатами
ее фокус находится в точке с координатами 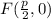
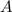 находиться в системе уравнения
находиться в системе уравнения 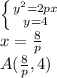 Если уравнение касательной равна
Если уравнение касательной равна 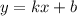 с учетом того что она проходит через точку
с учетом того что она проходит через точку 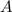 получаем
получаем 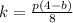 , подставляя
, подставляя 
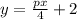
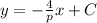 он проходит через точку
он проходит через точку 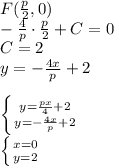
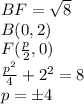
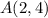
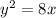
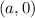 центр окружности (так как центр лежит на оси
центр окружности (так как центр лежит на оси 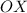 )
) 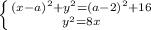
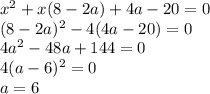
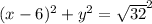
S -расстояние ав
v1-ск велосипедиста
v2-ск пешехода
t1-встречное движение
t2-движение в одном направлении
встречное движение
S=v1t1+v2t1=t1(v1+v2) (1)
S=v1t2-v2t2=t2(v1-v2) (2)
разделим (1) на (2) или наоборот
S/S = t1(v1+v2) /t2(v1-v2)
1 =t1(v1+v2) /t2(v1-v2)
t2/t1 =(v1+v2) /(v1-v2) <по условию t2/t1=5
5=(v1+v2) /(v1-v2)
5 (v1-v2) = (v1+v2)
5v1-5v2 = v1+v2
5v1-v1=5v2+v2
4v1=6v2
v1/v2=6/4=1.5 в 1.5 раза больше
ОТВЕТ в 1.5 раза скорость велосипедиста больше скорости пешехода