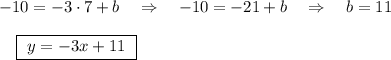ответ:[1;2]
Объяснение:
2х^2-6х+4≤0
Если графически решать данной неравенство то
y=2х^2-6х+4-это парабола ветви которой направлены вверх
y=0 - это ось Ох
Решением этого неравенства является область х в которой парабола лежит ниже
или касается в одной точке оси Ох
Но это возможно при D>=0 (а решением является отрезок [x1;x2])
Если D<0 решения нет и нет точек пересечения параболой оси Ох
Найдем D
D=36-32=4
x1=(6-2)/4=1
x2=(6+2)/4=2
Где х1 и х2- точки где парабола пересекает ось Ох
или 2х^2-6х+4 =0
2х^2-6х+4=2(x-1)(x-2)
Перепишем неравенство
2(x-1)(x-2)<=0
Тут можно решать любым методом
Решим методом интервалов.
Методом подстановки находим знаки левой части неравенства
+ 0 - 0 +.
!!
1 2.
Видно что левая часть неравенства меньше нуля в области
где х принадлежит [1;2]
ответ:[1;2]
ответ: y= -3x+11 .
Уравнение функции, описывающей прямо пропорциональную зависимость между переменнными "х" и "у" , такая:  .
.
Подставим координаты точки А(-4;12) в это равенство и найдём коэффициент k .
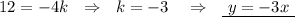
Линейная функция задаётся уравнением 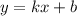 .
.
Так как график линейной функции параллелен графику прямой пропорциональности, то у этих функций будут равные угловые коэффициенты, то есть линейная функция будет иметь вид 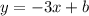
Найдём число "b" , подставив координаты точки D(7;-10) в уравнение линейной функции.