Решить уравнение! х+1.5/4=0.5х-0.25/6 1)-2.5 2)2.5 3)-2 4)2 чему равен х я

👇

Увидеть ответ

Ответ:

SERYK11

23.10.2021

избавляемся от дробей, получится 6х+9=2х-1
4х=-10

х=-2.5

4,6(6 оценок)

Ответ:

Timofry

23.10.2021

Преобразуешь уравнение ,Составляешь пропорцию

(2x+3)/8=(2x-1)/24

В итоге ты решишь должно получиться

х=-5/2

тоесть x=-2.5

4,7(53 оценок)

Открыть все ответы

Ответ:

irasurkova197

23.10.2021

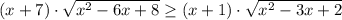
$(x+7)\cdot \sqrt{x^2-6x+8}\geq (x+1)\cdot \sqrt{x^2-3x+2}$

ОДЗ:

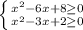
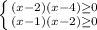$\left \{ {{x^2-6x+8 \geq0 } \atop {x^2-3x+2\geq 0 }} \right.$ $\left \{ {{(x-2)(x-4) \geq0 } \atop {(x-1)(x-2)\geq 0 }} \right.$ ⇒ $x \in (-\infty; 1] \cup 2 \cup [4; +\infty)$

Рассматриваем четыре случая с учетом ОДЗ:

1) Если правая часть неотрицательна, левая неположительна

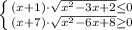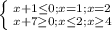$\left \{ {{(x+1)\cdot \sqrt{x^2-3x+2}\leq 0} \atop {(x+7)\cdot \sqrt{x^2-6x+8}\geq 0}} \right.$ ⇒ $\left \{ {{x+1\leq 0 ; x=1; x=2} \atop {\left \[ {{x+7 \geq 0; x\leq 2 ; x \geq 4 }} \right. }} \right.$ ⇒ $x \in [-7;- 1]$ U{1} U {2}

Неравенство верно при любых $x \in [-7;-1]$ U {1} U {2}

Если правая часть отрицательная, левая неотрицательная, неравенство неверно:

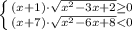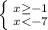$\left \{ {{(x+1)\cdot \sqrt{x^2-3x+2}\geq0} \atop {(x+7)\cdot \sqrt{x^2-6x+8}< 0}} \right.$ ⇒ $\left \{ {{x \geq-1} \atop {\left \[ {x$ ⇒ нет таких значений х

Если правая часть неотрицательная , левая неотрицательная

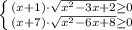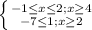$\left \{ {{(x+1)\cdot \sqrt{x^2-3x+2}\geq0} \atop {(x+7)\cdot \sqrt{x^2-6x+8}\geq 0}} \right.$ ⇒ $\left \{ {{-1\leq x\leq 2; x \geq4} \atop {\left \[ {-7 \leqx\leq1; x \geq2}} \right.$ ⇒ $x \in [-1;1] \cup2\cup[4;+\infty)$

возводим обе части неравенства в квадрат:

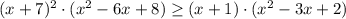
$(x+7)^2\cdot(x^2-6x+8)\geq (x+1)\cdot(x^2-3x+2)$

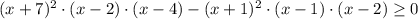
$(x+7)^2\cdot(x-2)\cdot (x-4)-( x+1)^2\cdot(x-1)\cdot (x-2)\geq 0$

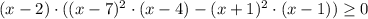
$(x-2)\cdot((x-7)^2\cdot (x-4)-( x+1)^2\cdot (x-1))\geq 0$

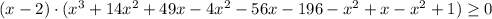
$(x-2)\cdot(x^3+14x^2+49x-4x^2-56x-196-x^2+x-x^2+1)\geq 0$

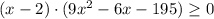
$(x-2)\cdot(9x^2-6x-195)\geq 0$

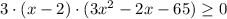$3\cdot (x-2)\cdot(3x^2-2x-65)\geq 0$ D=(-2)²-4·3·(-65)=784=28²

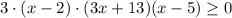
$3\cdot (x-2)\cdot(3x+13)(x-5)\geq 0$

$x \in [-\frac{13}{3} ;2] \cup[5;+\infty)$

C учетом условия третьего случая: $x \in [-1;1] \cup[4;+\infty)$

получим ответ третьего случая $x \in [-1;1] \cup [5;+\infty)$

Если левая часть отрицательная и правая тоже отрицательна

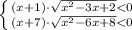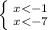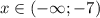
$\left \{ {{(x+1)\cdot \sqrt{x^2-3x+2}$ ⇒ $\left \{ {{x$ ⇒ $x \in (-\infty;-7)$

умножаем на (-1) обе части неравенства и

возводим в квадрат:

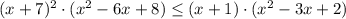
$(x+7)^2\cdot(x^2-6x+8)\leq (x+1)\cdot(x^2-3x+2)$

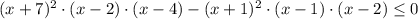
$(x+7)^2\cdot(x-2)\cdot (x-4)-( x+1)^2\cdot(x-1)\cdot (x-2)\leq 0$

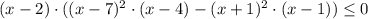
$(x-2)\cdot((x-7)^2\cdot (x-4)-( x+1)^2\cdot (x-1))\leq 0$

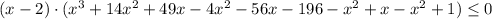
$(x-2)\cdot(x^3+14x^2+49x-4x^2-56x-196-x^2+x-x^2+1)\leq 0$

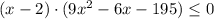
$(x-2)\cdot(9x^2-6x-195)\leq 0$

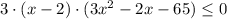
$3\cdot (x-2)\cdot(3x^2-2x-65)\leq 0$

D=(-2)²-4·3·(-65)=784=28²

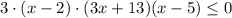
$3\cdot (x-2)\cdot(3x+13)(x-5)\leq 0$

$x \in (-\infty;-\frac{13}{3} ] \cup [2;5]$

C учетом условия четвертого случая: 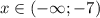$x \in (-\infty;-7)$

получим ответ четвертого случая 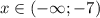$x \in (-\infty;-7)$

Объединяем ответы рассмотренных случаев:

$x \in (-\infty;1] \cup 2 \cup [5;+\infty)$

4,7(80 оценок)

Ответ:

Мила3287

23.10.2021

Схема 16 Факторы, влияющие на безопасность во внутреннем и выездном туризме На эту безопасность влияют следующие факторы (схема 16): опасные заболевания, которые можно получить на отдыхе (особенно в «экзотических» странах); травматизм и даже гибель людей во время занятий экстремальными, экзотическими и спортивными видами туризма (прежде всего альпинизм, скалолазание, горные лыжи, сноубординг, дайвинг); состояние преступности и меры, принимаемые для защиты туристов (террористическая деятельность, убийства, ограбления, кражи, мошенничества); в ряде стран (Бразилия, Кипр, Таиланд) принимаются дополнительные меры по защите иностранных граждан; состояние транспорта (наземного, воздушного, морского и речного); в некоторых странах аварии и катастрофы транспортных средств, перевозящих туристов, происходят достаточно часто; стихийные бедствия (землетрясения, извержения вулканов, ураганы, цунами, пожары, наводнения, сели, оползни, снежные лавины); осложнение внутриполитической ситуации в стране пребывания или в отдельном регионе; человеческий фактор (недостаточная правовая культура туристов, слабое знание ими правил личной безопасности). Туристы должны учитывать серьёзное различие между внутренним и международным туризмом. Находясь за рубежом, они являются иностранными гражданами. Поэтому они обязаны соблюдать законы страны пребывания, уважать её традиции и обычаи.

4,8(9 оценок)

Это интересно:

Финансы-и-бизнес

11.03.2020

Как создать инвестиционный план: шаг за шагом...

Компьютеры-и-электроника

30.09.2020

Как заглушить беспроводную сеть: 5 способов защиты вашей Wi-Fi сети...

Искусство-и-развлечения

19.08.2022

Как правильно танцевать джайв: основы и советы...

Кулинария-и-гостеприимство