Необходимо начертить вектор АВ=(2;4) . Начало вектора выбрать произвольно.
Координаты вектора - это проекции вектора на оси ОХ и ОУ. То есть вектор АВ проектируется на ось ОХ в отрезок , длина которого равна 2 единицам, а на ось ОУ - в отрезок, длина которого 4 единицы. Причём, так как координаты положительные, то направление от проекции начала вектора к проекции конца вектора такое же, как и у осей координат.
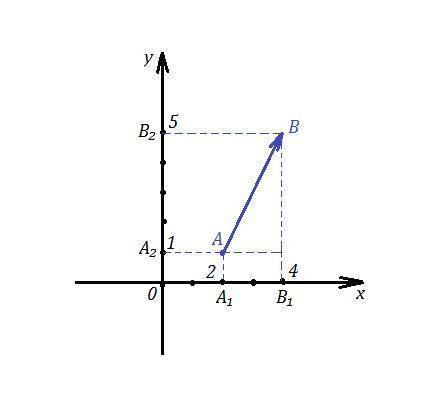
Если , например, за начало вектора возьмём точку А(2,1), то от точки А₁(2,0) , которая является проекцией точки А на ось ОХ, отложим вдоль оси ОХ отрезок длиной 2 единицы в направлении оси ОХ, попадём в точку В₁(4,0), которая будет проекцией точки В на ось ОХ. А₁В₁ - проекция вектора АВ на ось ОХ.
Аналогично, от точки А₂(0,1) отложим вдоль оси ОУ отрезок длиной 4 единицы, попадём в точку В₂(0,5) . А₂В₂ - проекция вектора АВ на ось ОУ.
Затем соединим точку А(2,1) с точкой В(4,5), получим вектор АВ=(2,4).
ответ: 1358114
Объяснение:
1. Делители числа 2019:
2019|3
673|673
1|
2. Взаимно простыми с 2019 являются все числа, не превосходящие 2019. не включая числа, кратные 3 и 673.
3. Имеется 673 числа, кратных 3, и число 673 - простое.
4. Сумма всех чисел от 1 до 2019, вычисляется методом Гауса, парами:
1-я пара: 1+2019=2020
всего пар: 2019/2=1009(ост.1) - значит среднее число 1010 пары не имеет.
Сумма всех чисел = 2020*1009+1010=2039190
5. Сумма всех чисел, кратных 3 вычисляется по формуле суммы членов ариaметической прогрессии:
a₁=3; d=3
а₆₇₃=2019 - известно, потому, что последний член заданного множества натуральных чисел от 1 до 2019, кратен 3. (2019/3=673)
S₆₇₃=(3+2019)|2*673
S₆₇₃=680403
6. Сумма всех натуральных чисел, не превосходящих 2019 и взаимно простых с ним:
2039190-680403-673=1358114
корни: x1=(-5+1)/6=2/3
x2=(-5-1)/6=-1