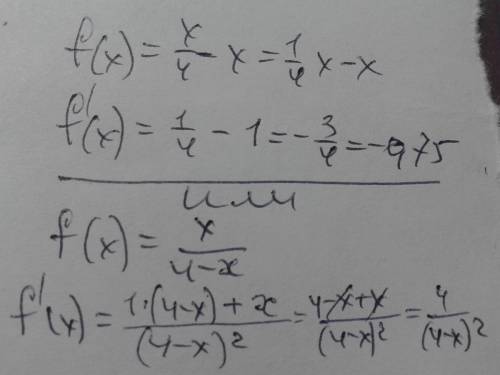
1) x²-6x-7=0.
по т. виета:
х1= 7, х2= -1.
ответ: -1; 7.
2) 2х²-3х+1=0;
d= b²-4ac= 9-9=0 => один корень.
х= (3+0)/4= ¾.
ответ: ¾.
3) 5х²+2х-3=0;
d= 4+60=64=8².
x1= (-2+8)/10= 6/10= 0,6
x2= (-2-8)/10= -10/10= -1.
ответ: -1; 0,6.
4) 2х²+5х-7=0;
d= 25+56= 81=9².
x1= (-5+9)/4= 4/4= 1.
x2= (-5-9)/4= -14/4= -7/2= -3½= -3,5.
ответ: -3,5; 1.
5) х²-8х-9=0;
по т. виета:
х1= 9, х2= -1.
ответ: -1; 9.
6) х²-х-2=0;
по т. виета:
х1= 2, х2= -1.
ответ: -1; 2.
7) х²+3х-4=0;
по т. виета:
х1= -4, х2= 1.
ответ: -4; 1.
p.s. все формулы смотреть во вложении, если теорему виета не учили, делаете все по формуле через дискриминант, как это было у меня в половине примеров! есть вопросы -
Объяснение:
Выносим общий множитель √2*sinx за скобки
√2*sinx*(2-cosx)+cosx-2=0
Выносим знак минус за скобку
√2*sinx*(2-cosx)-(2-cosx)=0
Выносим за скобку общий множитель 2-cosx
(2-cosx)*(√2*sinx-1)=0
2-cosx=0 или √2*sinx-1=0
1) -cosx=-2 - не существует, поскольку cosx принадлежит [-1:1]
2) √2*sinx=1 делим на √2
sinx= 1/√2
sinx= 1/√2
используем обратную тригонометрическую ф-цию
x=arcsin(1/√2)
sinx периодическая ф-ция добавляем 2Пn, n принадлежит Z
x=arcsin(1/√2)+2Пn, n принадлежит Z
Решаем уравнение
x=п/4+2Пn, n принадлежит Z
Вроде так