Для вычисления понадобятся следующие определения и формулы.
arcsin b = α
Арксинусом числа b∈[-1; 1] называется угол α такой, что
sin α = b и 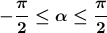 .
.
arcsin (sin α) = α, если ![\boldsymbol{\alpha \in \Big[-\dfrac{\pi }{2}; \dfrac{\pi }{2}}\Big]](/tpl/images/0315/2594/4cc60.png)
sin (arcsin b) = b, где b∈[-1; 1]
cos (arcsin b) ≥ 0 и 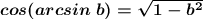 , b∈[-1; 1]
, b∈[-1; 1]
sin (2α) = 2 sin α · cos α
=====================================================
sin (2arcsin 0,75) = 2 · sin(arcsin 0,75) · cos (arcsin 0,75)
0,75∈[-1; 1] ⇒ sin(arcsin 0,75) = 0,75 = 3/4
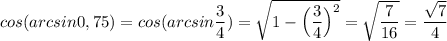
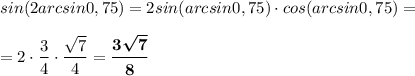
===================================================
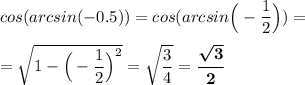
===================================================
arcsin (sin2)
Так как 2 > π/2 ≈ 1,57, то есть 2∉[-π/2; π/2] , то нельзя сразу воспользоваться формулой arcsin (sin α) = α. Нужно преобразовать выражение с формул приведения.
arcsin (sin 2) = arcsin (sin (π - 2)) = π - 2
После преобразования угол (π - 2) ≈1,14 ∈ [-π/2; π/2]
Для вычисления понадобятся следующие определения и формулы.
arcsin b = α
Арксинусом числа b∈[-1; 1] называется угол α такой, что
sin α = b и 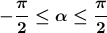 .
.
arcsin (sin α) = α, если ![\boldsymbol{\alpha \in \Big[-\dfrac{\pi }{2}; \dfrac{\pi }{2}}\Big]](/tpl/images/0315/2594/4cc60.png)
sin (arcsin b) = b, где b∈[-1; 1]
cos (arcsin b) ≥ 0 и 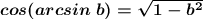 , b∈[-1; 1]
, b∈[-1; 1]
sin (2α) = 2 sin α · cos α
=====================================================
sin (2arcsin 0,75) = 2 · sin(arcsin 0,75) · cos (arcsin 0,75)
0,75∈[-1; 1] ⇒ sin(arcsin 0,75) = 0,75 = 3/4
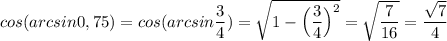
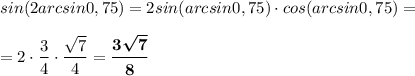
===================================================
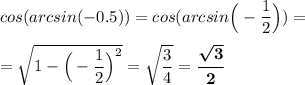
===================================================
arcsin (sin2)
Так как 2 > π/2 ≈ 1,57, то есть 2∉[-π/2; π/2] , то нельзя сразу воспользоваться формулой arcsin (sin α) = α. Нужно преобразовать выражение с формул приведения.
arcsin (sin 2) = arcsin (sin (π - 2)) = π - 2
После преобразования угол (π - 2) ≈1,14 ∈ [-π/2; π/2]
у - количество станков 2-го типа
По условию
х - у > 5
Имеем систему двух неравенств
{13x + 12y ≤ 305
{15x +24y > 438
Решаем методом сложения
Первое неравенство умножим на 2, а второе умножим на (-1),
{13х*2 + 12у*2 ≤ 305*2
{15х*(-1) + 24у*(-1) < 438*(-1)
Сложим эти неравенства
26х + 24у - 15х - 24у ≤ 610 - 438
11х ≤ 172
х ≤ 172 : 11
х ≤ 15,6
Ближайшее целое х= 15 - количество станков 1-го типа
По условию х > y более, чем на 5, т.е минимум на 6 и более, поэтому проверим у=15-6=9
у=9 - количество станков 2-го типа
Проверка значений х=15; у= 9
{13 * 15 + 12 * 9 ≤ 305
{15*15 + 24*9 > 438
Считаем
{195 + 108 ≤ 305 => 303 ≤ 305 - верное неравенство
{225 + 216 > 438 => 441 > 438 - верное неравенство
ответ; 15 станков 1-го типа;
9 станков 2-го типа