![\displaystyle p(x)= \left \{ {{ \dfrac{1}{b-a},~~~ x\in [a;b] } \atop {0~~~ ~~~,~~x\notin [a;b]}} \right.](/tpl/images/0836/3813/a72ca.png)
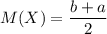
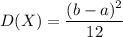
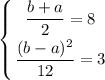получим: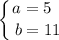 
![p(x)=\displaystyle \left \{ {{ \frac{1}{6},~~~ x\in[5;11] } \atop {0,~~~ x\notin[5;11]}} \right.](/tpl/images/0836/3813/eadb5.png)
график функции можно получить из графика параболы, оставив на месте часть, где функция больше 0 и симметрично отразив относительно Оx другую часть, где функция меньше 0, т.е.
график парабола
находим x вершину =2/2=1
находим y вершину = 1*1-2*1-3=-4
сначалс строим график обычной параболы
затем часть параболы ниже оси x отражаем относительно оси x (переворачиваем)
получаем что-то похожее на w - это график модуля этой параболы
т.к. перед функцией стоит знак - , то отображаем весь график относительно оси x
получаем что-то похожее на м
прямая y=m пересекает этот график ровно в трех точках при x=-4 (где вершина и ветки графика)
2) Ix-2I<5 x-2<5 x<7 -x+2<5 x>-3 ⇒ x∈(-3;7).
3) √(x(x²-9))
ОДЗ: x(x²-9)≥0 x(x-3)(x+3)≥0
-∞-___-3+0-3++∞
x[-3;0]U[3;+∞).
4) (2x+3)(x-x²)/(6-x)≥0
x(2x-3)(1-x)/(6-x)≥0
-∞+0-1+1,5-6++∞
x∈(-∞;0]U[1;1,5]U[6;+∞).
5) (2x-3)(4-x)(x+8)≥0
-∞+-8-1,5___+4-+∞
x∈(-∞;-8]U[1,5;4].
6) (2-5x)/(x+3)≥0
-∞-___-3+0,4-+∞
x∈[-3;0,4] ⇒ x=-3, -2, -1, 0.