
Задание № 1:
Найдите последнюю ненулевую цифру значения произведения 40^50*50^40?
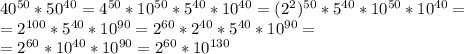
10^130 нас не интересует. Попробуем повозводить 2 в степень:
2^1=2, 2^2=4, 2^3=8, 2^4=16, 2^5=32
Пятая степень, как и первая, оканчивается на 2. Образуется своего рода цикл.
Чтобы узнать последнюю цифру степени N, нужно N разделить на 4. Остаток от деления соответствует степени, последняя цифра которой совпадает с последней цифрой степени N. Остаток 0 соответствует 4-ой степени.
60/4=15, остаток 0 – 4 степень оканчивается на 6, значит и 60 степень оканчивается на 6
ОТВЕТ: 6
Задание № 3:
Сколько корней имеет уравнение: |x|=|x−1|+x−3?
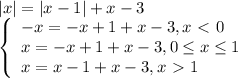
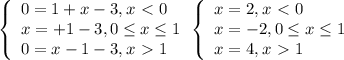
Условию раскрытия модуля соответствует только третья строчка.
ОТВЕТ: 1
ответ: окончательным ответом будет (-25x^2-12x+25) / (-25x^2+5x)
Объяснение:
Сначала делаем то, что в скобках, а в скобках определяем главное. Сперва скобки и умножение. Под общий знаменатель, но сначала представим 25x^2-1 как две скобки 5х-1 и 5х+1. Далее из числителя 5х^2+х выносим за скобки х и получится х(5х+1). Разложим второй знаменатель х^3+125=(х+5)(x^2-5х+25). Если заменить знаменатели и числители на полученные выражения, то будут сокращения и получится дробь: 1/(5х-1) * х/(х+5). под общий знаменатель (5х-1)(х+5) так как между дробями УМНОЖЕНИЕ, то в числителе ничего НЕ меняется.
Второй шаг это из полученной выше дроби вычитаем другую дробь.
x\((x+5)*(5x-1)) - (x+5)\(5x^2-x) из знаменателя второй дроби выносим x. далее под общий знаменатель x(x+5)(5x-1) , числитель тогда x^2-(x+5)^2. Далее разложим x+5 и все в квадрате. x^2- x^2-10x-25 (cкобку сразу раскрываем). Сокращаем противоположные слагаемые (это допустим -5фа и 5аф ) выносим "-" перед дробь, потом раскрываем скобки в знаменателе, приводим подобные члены Должно получится: -(10x+25)/(5x^3+24x^-5x)
Это уже ответ полученный из скобок. Эту дробь мы делим на 5x/(x^2+5x). При делении вторая дробь переворачивается и деление становится умножением, поэтому полученную из скобок дробь мы умножаем на (x^2+5x)/5x
(5x^3+24x^-5x) представим как (x^2+5x)(5x-1)
(10x+25) представим как 5(2х+5)
в итоге:
- (5(2х+5))/(x^2+5x)(5x-1) * (x^2+5x)/5x сокращаем х^2+5x и пятерки.
получится: - (2x+5)/(5x-1)*1/x = -(2x+5)/(5x^2-x) - это ответ деления скобки на дробь.
дальше из полученной выше дроби вычитаем (25х+22)/(5-25х)