1) 45 мин=0.75 часа
2) 80*0.75=60 км - расстояние между автомобилями в момент выезда второго автомобиля
3) 90+80=170 км\час - сумма скоростей(на столько км в час сокращается расстояние между автомобилями)
4)400-60=340 км - осталось проехать автомобилям до встречи
5) 340:170=2 час- через столько времени после выезда второго автомобиля состоится встреча
5) 2*90=180 км - такое расстояние проедет второй автомобиль до встречи
6) 400-180=220 км - на таком расстоянии от города А автомобили встретятся
ответ: на расстоянии 220 км
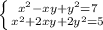
Сложим первое уравнение,домноженное на 2 со вторым:
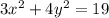
Очевидно,что x и y не обращаются в ноль,так как число 19 простое и не имеет делителей на интервале (1;19)
Значит:
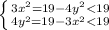
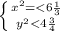
![\left \{ {{|x| \in [1;2]} \atop {|y| \in [1;2]}} \right](/tpl/images/0099/8562/6984c.png)
Из полученных отрезков лишь пара значений модулей удовлетворяет нашему уравнению:
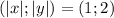
Осталось лишь раскрыть модуль,сделаем это следующим образом:
Рассмотрим полиномы вида:
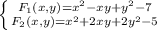
Подставим модули корней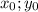 
под степени 2,так как они являются четными и не меняют значение:
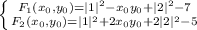
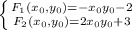
Очевидно,что для старших мономов вида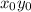 
обоих полиномов для обращения последних в ноль определен отрицательный знак.Это выполнимо в случае только одного отрицательного и одного положительного переменного.
Значит возможные целочисленные значения решения исходной системы:
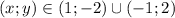
(x-0,5)(x+2)³-(x-0,5)(x-1)³-9(x-0,5)=0
(x-0,5)·((x+2)³-(x-1)³-9)=0 [/tex]
(x-0,5)·(x+2-(x-1))·((x+2)²+(x+2)(x-1)+(x-1)²-9)=0
(x-0,5)·(x+2-x+1)·(x²+4x+4+x²+2x-x-2+x²-2x+1-9)=0
(x-0,5)·3·(3x²+6x-6)=0
(x-0,5)·9·(x²+2x-2)=0
x-0,5=0 или х²+2х-2=0
х=0,5 D=4+8=12
x=(-2-√12)/2 =-1-√3 или х=(-2+√12)/2 =-1+√3
Среднее арифметическое корней
(0,5+( -1-√3)+( -1+√3))/3=-1,5/3=-0,5
ответ. -0,5