48
Объяснение:
Для начала изобразим это число как определенное количество позиций:
_ _ _ _ _
На каждой позиции мы будем записывать сколько цифр на этой позиции может стоять. Потом, чтобы найти количество чисел, мы переумножим значения этих позиций.
Так как все цифры разные, на пятой позиции может стоять одна из пяти цифр, на четвёртой одна из четырёх оставшихся, на третей одна из трёх, на второй одна из двух, и одна на первой. То есть, значения позиций выглядели бы так:
1 2 3 4 5
Но, также известно, что числа должны быть парными, а значит на последней позиции может находится только одна из двух цифр:
1 2 3 4 2
Соответсвенно, переумножением отмеченных этих цифр мы получим количество вариантов:
1 × 2 × 3 × 4 × 2 = 48
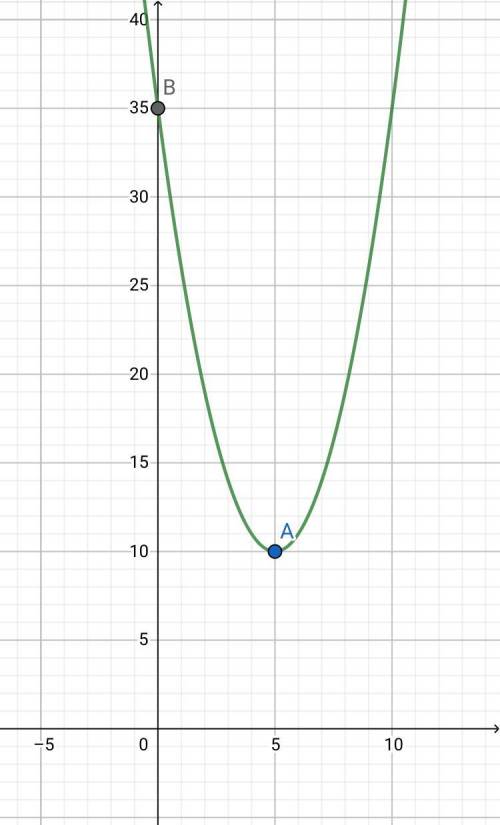
f(x) = (x-5)² + 10 = x² - 10x + 35
а) Высоту? Это как понять. Парабола не имеет высоты. Парабола бесконечна, начиная от вершины.
Возможно, Вы имели в виду найти вершину параболы?
Вершина параболы - точка А(х₀; у₀)
х₀ = -b/2a = 10/2 = 5
у₀ = f(х₀) = 10
A(5; 10)
b) f(x) = (x-5)² + 10
(x-5)² <— это значит что функция х² смещена на пять единиц вправо
Соответсвенно, ось симметрии будет иметь вид:
х = 5
с) f(x) = 0
(x-5)²>= 0
(x-5)² + 10 >= 10
А значит, значение функции попросту не может быть равно 0.
То есть, точек пересечения с осью Ох нет.
d) х = 0
f(x) = x² - 10x + 35 = 35
Точка пересечения с осью Оу - точка В
В(0; 35)
e) —> в прикрепленном файле
Автомобиль проехал 4/9 пути, т.е. 4/9 · 1620 = 720 км, после чего ему осталось проехать 1620 - 720 = 900 км.
Пусть х км/ч - скорость автомобиля после задержки, тогда х - 5 км/ч - его скорость до задержки. 900 км пути он проехал за 900/х часов, а должен был проехать за 900/(х - 5) часов. По условию задачи он ехал на 900/(х - 5) - 900/х часов меньше чем должен был и эта разность равна 2 часа. Имеем уравнение.
900/(х - 5) - 900/х = 2| ·(x-5)x, x≠5, x≠0.
900x - 900(x-5) = 2x(x-5);
900x - 900x+4500 = 2x² - 10x;
2x² - 10x - 4500 = 0;
x² - 5x - 2250 = 0.
D = 25 + 4·2250 = 25(1 + 360) = 25·361; √D = √(25·361) = 5·19 = 95
x₁ = (5 + 95)/2 = 50; x₂ = (5 - 95)/2 = -45 - не удовлетворяет условие задачи.
ответ: 50 км/ч.