ответ:Привет!
Первоначально надо найти корни квадратного уравнения в числителе дроби
Корни квадратного уравнения можно решить последовательно рассчитывая дискриминант, значение которого должно быть больше или равно нулю (при нуле x1=x2), после - значения корней.
а*X^2+b*X+c=0
D=b*b-4*a*c ; x1=[-b-(D^(1/2))]/(2*a) и x2=[-b+(D^(1/2))]/(2*a)
Если D=0, то x1,2=-b/(2*a)
Теперь конкретно:
1) Числитель дроби
3x2 -7x +2=0
D=(-7)*(-7)-4*2*3=49-24=25
x1=[7-5]/(2*3)=2/6=1/3 и x2=[7+5]/(2*3)=12/6=2
3x2 -7x +2=(3x-1)*(x-2)
2) Знаменатель дроби
2-6х=2*(1-3х) Вынесем -1 за скобку, получим -2*(3x-1)
Имеем дробь [(3x-1)*(x-2)]/[-2*(3x-1)]
Здесь можно сократить на (3x-1)
После сокращения получаем [(x-2)]/[-2] или -0,5*(x-2)
ОТВЕТ: -0,5*(x-2)
Успехов!
Объяснение:Привет!
Первоначально надо найти корни квадратного уравнения в числителе дроби
Корни квадратного уравнения можно решить последовательно рассчитывая дискриминант, значение которого должно быть больше или равно нулю (при нуле x1=x2), после - значения корней.
а*X^2+b*X+c=0
D=b*b-4*a*c ; x1=[-b-(D^(1/2))]/(2*a) и x2=[-b+(D^(1/2))]/(2*a)
Если D=0, то x1,2=-b/(2*a)
Теперь конкретно:
1) Числитель дроби
3x2 -7x +2=0
D=(-7)*(-7)-4*2*3=49-24=25
x1=[7-5]/(2*3)=2/6=1/3 и x2=[7+5]/(2*3)=12/6=2
3x2 -7x +2=(3x-1)*(x-2)
2) Знаменатель дроби
2-6х=2*(1-3х) Вынесем -1 за скобку, получим -2*(3x-1)
Имеем дробь [(3x-1)*(x-2)]/[-2*(3x-1)]
Здесь можно сократить на (3x-1)
После сокращения получаем [(x-2)]/[-2] или -0,5*(x-2)
ОТВЕТ: -0,5*(x-2)
Успехов!
Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2) 
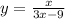. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б) 
при 
Если x = -5, то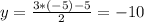 
Если х= 3, то 
Значит, 
-4a=-5|/-4
a=1,25