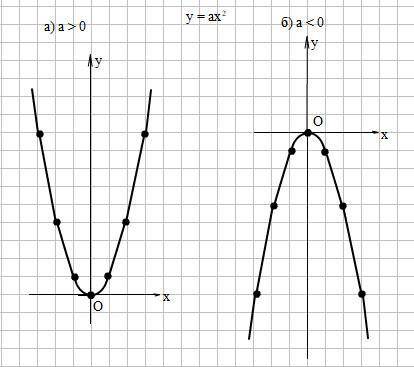
График функции у = ах² - парабола (смотри рисунок на фото)
а) а >0
Область определения D(y) = (-∞; +∞)
Область значений Е(у) = [0; +∞)
Наибольшего значения не существует
Наименьшее значение при х = 0 у наим= 0
Нуль функции единственный в точке с координатой х = 0
При х∈(-∞; 0] у ↓ (функция убывает)
При х∈[0; +∞) y↑ (функция возрастает)
у > 0 при х∈(-∞; 0) U (0; +∞)
б) a < 0
Область определения D(y) = (-∞; +∞)
Область значений Е(у) = (-∞; 0]
Наименьшего значения не существует
Наибольшее значение при х = 0 у наиб= 0
Нуль функции единственный в точке с координатой х = 0
При х∈(-∞; 0] у ↑ (функция возрастает)
При х∈[0; +∞) y↓ (функция убывает)
у < 0 при х∈(-∞; 0) U (0; +∞)
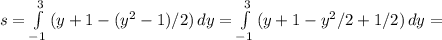
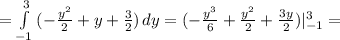
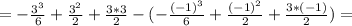
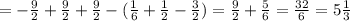 ед².
ед². 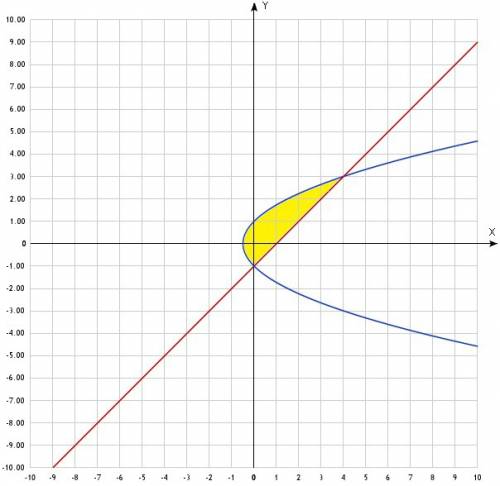
Объяснение:
свойства функции у = ах² при а > 0:
Область определения функции (-∞; ∞). при х = 0, у = 0. Значит график проходит через начало координат. при х ≠ 0, у > 0, значит график расположен в верхней полуплоскости. Функция четная Функция убывает в промежутке (-∞; 0] и возрастает в промежутке [0; ∞). Наименьшее значение у = 0 функция принимает при х = 0, наибольшего значения функция не имеет. Область значений функции это промежуток [0; +∞).свойства функции у = ах² при а < 0:
Область определения функции (-∞; ∞). при х = 0, у = 0. Значит график проходит через начало координат. при х ≠ 0, то у < 0. Значит график расположен в нижней полуплоскости. Функция четная, у(-х) = y(x). Функция возрастает в промежутке (-∞; 0] и убывает в промежутке [0; ∞). Наибольшее значение у = 0 функция принимает при х = 0, наименьшего значения функция не имеет. Область значений функции - промежуток (-∞; 0].