
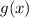 ;
; ;
; и будет искомой фигурой.
и будет искомой фигурой.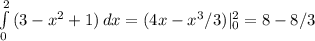
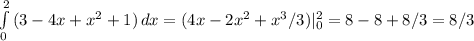
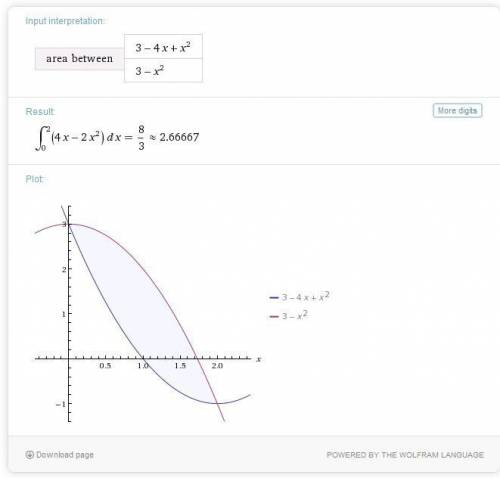
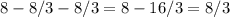 (кв. ед.)
(кв. ед.)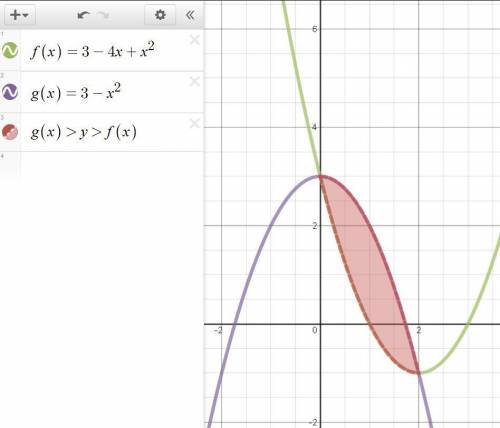
Дробь  является неправильной рациональной дробью, так как степени многочленов в числителе и в знаменателе одинаковые и равны 1. Значит можно выделить целую и дробную часть неправильной дроби. Так как в знаменателе стоит многочлен 1 степени (линейная ф-ция) х+1, то и в числителе выделим х+1. Для этого надо вынести за скобки коэффициент (-5), который стоит перед х, и записать в скобках (х+1). Так как -5(х+1)=-5х-5, то , чтобы выражение не изменилось, надо добавить (+5), получим:
является неправильной рациональной дробью, так как степени многочленов в числителе и в знаменателе одинаковые и равны 1. Значит можно выделить целую и дробную часть неправильной дроби. Так как в знаменателе стоит многочлен 1 степени (линейная ф-ция) х+1, то и в числителе выделим х+1. Для этого надо вынести за скобки коэффициент (-5), который стоит перед х, и записать в скобках (х+1). Так как -5(х+1)=-5х-5, то , чтобы выражение не изменилось, надо добавить (+5), получим:
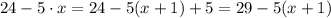 .
.
Если в дальнейшем надо записать целую и дробную части неправильной рац. дроби, то
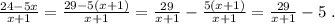
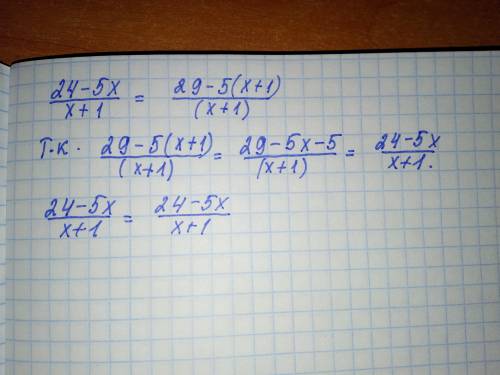
16=4²
64=2⁶
256=2⁸
2) 0,09=0,3²
0,027 = 0,3³
0,00243 = 0,3⁵