1. Напишите уравнение прямой, проходящей через заданные точки: A (2; 1) B (-1; 2). [2 балла]
2. Найти координаты и радиус центра круга в соответствии с заданным уравнением: (x-4) 2 + (y + 8) 2 = 36 [1 балл]
3. Очки даны.
а) опираться на координаты потолков; [1 балл]
б) найти длину стен; [3 балла]
в) определить тип (равносторонний, равносторонний, прямоугольный); [2 балла]
г) Рассчитать площадь данного треугольника. [2 балла]
4. Найдите площадь прямоугольника с вершинами A (1; -1) B (0; 1) C (4; 3) и D (5; 1) и докажите, что это прямоугольник. Сделать это:
а) нарисуйте схему координат потолков; [1 балл]
б) найти длину стен; [4 балла]
в) определить и доказать диагонали; [2 балла]
г) Рассчитайте площадь прямоугольника. [2 балла]
Объяснение:
памагитеееВ решении.
Объяснение:
Даны точки B (-3;-4) и C(6;3).
1) Проходит ли график функции y = 19/x через точку C?
Нужно в уравнение подставить известные значения х и у (координаты точки). Если левая часть равна правой, то проходит, и наоборот.
y = 19/x; C(6;3);
3 = 19/6
3 ≠ 3,2, не проходит;
y = 19/x; B (-3;-4);
-4 = 19/-3
-4 ≠ -6,3, не проходит.
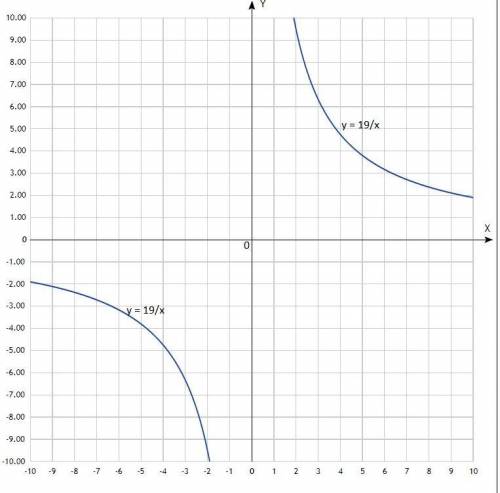
2) Построить график.
График - гипербола.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -10 -8 -6 -4 -2 -1 0 1 2 4 6 8 10
у -1,9 -2,4 -3,2 -4,8 -9,5 -19 - 19 9,5 4,8 3,2 2,4 1,9
По вычисленным точкам построить график.
2(х - 8у)
2*х - 2*8у= 2х-16у
изи в 6 классе уже знаю