Квадратное уравнение можно представить как P(x)=0, где P(x) - квадратных трёхчлен. Его можно разложить на множители (если есть совпадающие или различные корни) и получится a(x-x1)(x-x2), где a - старший коэф. P(x), а x1 и x2 корни уравнения. "a" может быть любым число, кроме 0, для удобства в решении используем a=1.
1) (x-2)(x-7) = x²-2x-7x+14
x²-9x+14=0 - квад. уравнен.
2) (x-(-1))(x-4) = x²+x-4x-4
x²-3x-4=0
3) (x-(-3))(x-(-4)) = x²+3x+4x+12
x²+7x+12=0
4) (x-0)(x-6) = x²-6x
x²-6x=0
5) (x-(-5))(x-5) = x²-5²
x²-25=0
6) (x-9)(x-9) = x²-2·9x-9²
x²-18x+81=0
7)
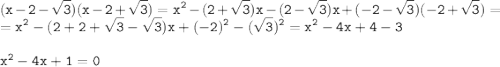
8)
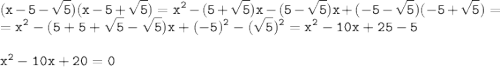
9)
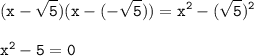
10) (x-0)(x-0) = x²
x²=0
216x^3 - 1 = (6x)^3 - 1^3 = (6x-1)(36x^2+6x+1)
100b^2 - 140bx^2 + 49x^4 = (10b - 7x^2)^2=(10b-7x^2)(10b-7x^2)
125b^3 + 27 = (5b + 3)(25b^2 - 15b + 9)
(5a - 1/5)^2 = 25a^2 - 2a + 1/25)
(3a - 5b^2)(9a^2 + 15ab^2 + 25b^4) = (3a)^3 - (5b^2)^3 = 27a^3 - 125b^6
(0,8x+ 5)(5 - 0,8x) = (5 + 0,8x)(5 - 0,8x) = 5^2 - (0,8x)^2 = 25 - 0,64x^2
(7x+ 0,4)^2 = 49x^2 + 5,6x + 0,16
(6y + 1)(36y^2 - 6y + 1) = (6y)^3 + 1^3 = 216y^3 + 1
25x^2 + 60xy + 36y^2 = (5x + 6y)^2 = (5x + 6y)(5x + 6y).