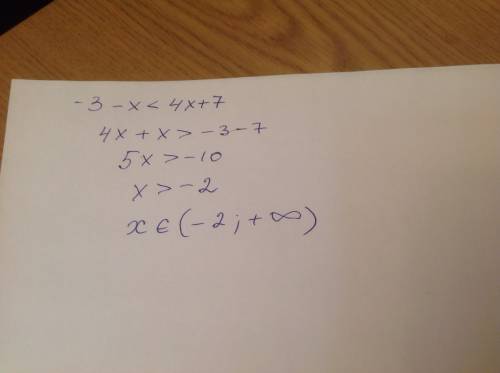
Відповідь:
Пояснення:
1.
а) ні
б) так
в) ні
г) так
=========================
2.
а) y = -3x + 2 при x = 5, y - ?
y = -3 * 5 + 2 = -15 + 2 = -13
б) y = -3x + 2 при y = 8, x - ?
8 = -3x + 2
3x = 2 - 8 = -6
x = -6/3 = -2
=========================
3. на фото нижче
=========================
4. y = -0,2x + 1,8
а) нулі функції - ?
0 = -0,2x + 1,8
0,2x = 1,8
x = 1,8/0,2 = 9
б) N(-6; -3), де x = -6, y = -3
-3 = -0,2*-6 + 1,8 = 1,2 + 1,8 = 3 - неправда, а це означає що графік не проходить через точку N.
=========================
5.
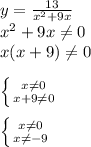Відповідь: х∈(-∞;-9)∪(-9;0)∪(0;+∞)
=========================
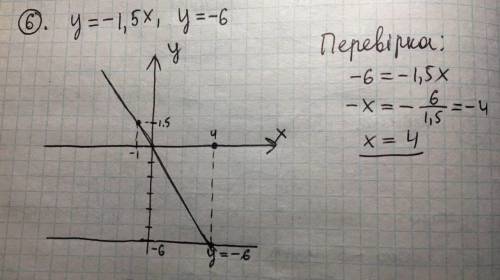
6. на фото нижче
=========================
7. на фото нижче
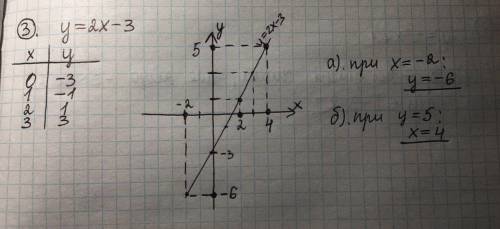
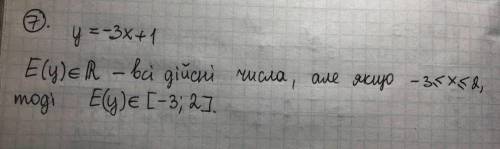
Возведем обе части равенства x + y + z = 0 в квадрат. Получим (x + y + z)² = 0 => (x + y)² + 2(x + y)z + z² = 0 => x² + 2xy + y² + 2xz + 2yz + z² = 0 => x² + y² + z² = -2(xy + xz + yz). Возведем обе части последнего равенства в квадрат. Получим (x² + y² + z²)² = 4(xy + xz + yz)² = 4((xy + xz)² + 2(xy + xz)yz + y²z²) = 4(x²y² + 2x²yz + x²z² + 2y²xz + 2z²xy + y²z²) = 4(x²y² + x²z² + y²z² + 2xyz(x + y + z)) = 4(x²y² + x²z² + y²z²), т. к. x + y + z = 0. С другой стороны (x² + y² + z²)² = ((x² + y²)² + 2(x² + y²)z² + z⁴) = x⁴ + 2x²y² + y⁴ + 2x²z² + 2y²z² + z⁴ = x⁴ + y⁴ + z⁴ + 2(x²y² + x²z² + y²z²). Тогда (x² + y² + z²)² = 4(x²y² + x²z² + y²z²) = x⁴ + y⁴ + z⁴ + 2(x²y² + x²z² + y²z²) => x⁴ + y⁴ + z⁴ = 2(x²y² + x²z² + y²z²). Отсюда получаем требуемое равенство (x² + y² + z²)² = x⁴ + y⁴ + z⁴ + 2(x²y² + x²z² + y²z²) = x⁴ + y⁴ + z⁴ + x⁴ + y⁴ + z⁴ = 2(x⁴ + y⁴ + z⁴).
