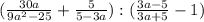
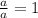, что 
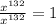, и что даже 
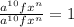. Выходит, что и 
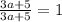. А теперь внимание на тот шаг, когда единицу мы представили в виде одинаковых значений для числителя и знаменателя, что и у знаменателя уменьшаемого числа. 
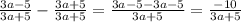, или равно 
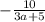. Что же, делитель стал выглядеть несколько изящнее, теперь разбираемся с делимым.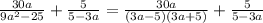 
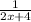равно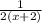 
, 
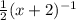и даже равно 
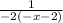, или равно 
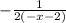, так? Выходит, что и 
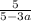равно 
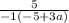, или равно 
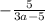. Однако не стоит забывать о том, что обыкновенные дроби нельзя складывать/вычитать, имея при этом разные знаменатели. Необходимо умножить числитель и знаменатель вычитаемого на 
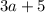, чтобы основания дробей обрели одинаковое значение: 
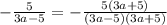. Теперь то можно складывать.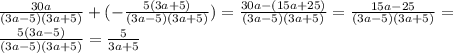 
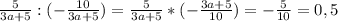
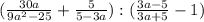равно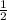 
при любом значении α.
8 - 3,7 = 4,3
4/7 * 7/8 = (1*1)/(1*2) = 1/2
4 2/7 : 1 1/7 = 30/7 : 8/7 = 30/7 * 7/8 = (15*1)/(1*4) = 15/4 = 3 3/4
4,8 : (7 + 3 * 3) = 4,8 : 16 = 0,3
3/7m + 2/7m + 4/7m - 2/7m = 7/7m = m