Нужно сравнить длины сторон треугольников
Для этого находим их по формуле расстояния между двумя точками
d=√((x2-x1)^2+(y2-y1)^2)
a)
AB=√((2+2)^2+(-1+1)^2)=√(16)=4
BC=√((-2-2)^2+(1+1)^2)=√(16+4)=√20
CA=√((-2+2)^2+(-1-1)^2)=√(4)=2
Стороны не равны, но сторона BC больше остальных, поэтому проверим выполняется ли на них теорема пифагора
(√20)^2=2^2+4^2
20=4+16
20=20
Теорема Пифагора выполняется, значит треугольник прямоугольный.
б)
AB=√((2+2)^2+(-2+2)^2)=√(16)=4
BC=√((0-2)^2+(1+2)^2)=√(4+9)=√13
CA=√((-2-0)^2+(-2-1)^2)=√(4+9)=√13
т.к. равны 2 стороны, то треугольник равнобедренный.
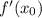производная функции в данной точке. А 
точка касания по иксу.
мы должны найти производную общего типа этой функции.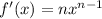
- где n это степень.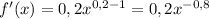
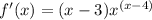
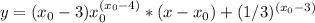
и получаешь уравнение касательной.
(Если после Х стоит большая 2 - это квадрат)
25х2 - 30х + 9 - 25х2 = 21
-30х + 9 = 21
-30х = 21-9
-30х = 12
х = -0,4 или