Вначале заметим, что функция непрерывна на всей области определения (при этом,  ).
).
Теперь найдем производную функции:

Потом - критические точки производной (то есть те, в которых производная не существует, - таких нет, - и те, в которых она обнуляется):

Осталось только расставить знаки производной:
///////////////////
+ + + + + + + ![\bigg [ \; - \dfrac{5}{3} \; \bigg ]](/tpl/images/1354/6534/6fa43.png) - - - - - - - - -
- - - - - - - - - ![\bigg [\; 1 \; \bigg ]](/tpl/images/1354/6534/d4832.png) + + + + + + + + + +
+ + + + + + + + + +
Если производная функции в данной точке отрицательна, то сама функция в этой точке убывает. Поэтому искомый промежуток (ставим квадратные скобки, так как было выяснено раньше, что функция непрерывна на всей области определения):
![x \in \bigg [ \; - \dfrac{5}{3} ; \; 1 \; \bigg ]](/tpl/images/1354/6534/82fed.png)
Задача решена!
ответ:![\bold {{\bigg [ \; - \dfrac{5}{3} ; \; 1 \; \bigg ]}}](/tpl/images/1354/6534/32e63.png)

-П; -33П/32; -41П/32; -43П/32; -35П/32
Объяснение:
cos 9x - cos 7x = √2*sin x
Найти корни на отрезке [-3П/2; -П]
Есть формула разности косинусов:
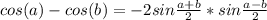
Подставляем:
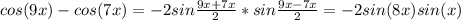
Подставляем в наше уравнение:
-2sin 8x*sin x = √2*sin x
0 = √2*sin x + 2sin 8x*sin x
sin x*(√2 + 2sin 8x) = 0
1) sin x = 0; x = Пk.
На указанном отрезке будет корень
x1 = -П
2) √2 + 2sin 8x = 0
sin 8x = -√2/2
8x = -П/4 + 2Пk; x = -П/32 + Пk/4
На указанном отрезке [-3П/2; -П] = [-48П/32; -32П/32] будут корни:
x2 = -П/32 - П = -33П/32
x3 = -П/32 - 5П/4 = -41П/32
3) sin 8x = -√2/2
8x = 5П/4 + 2Пk
x = 5П/32 + Пk/4
На указанном отрезке [-3П/2; -П] = [-48П/32; -32П/32] будут корни:
x4 = 5П/32 - 6П/4 = -43П/32
x5 = 5П/32 - 5П/4 = -35П/32