Требуется огородить прямоугольный участок земли так, чтобы при данном кол-ве погонных метров изгороди, равной 100 м, площадь участка была наибольшей. найдите стороны этого участка. отличники, !
Площадь прямоугольного треугольника равна произведение катетов деленное на 2
Обозначим катеты за A и B, гипотинузу за C. И так как сумма углов треугольника равна 180 градусов, то получается третий, неизвестный угол равен 180-90-15=75 градусов
По теореме косинусов: a^2=b^2+c^2-2bcCos(15)
по теореме Пифагора: a^2+b^2=c^2
Получается система уравнений: a^2=b^2+16-2*4*b*0,9659 a^2+b^2=16
P = m/n. Пространство исходов упорядоченные пары чисел от 1 до 6, например: (1;6); (2;3), (6;5) и т.п. Всего таких исходов n = 6*6, A) m = 5*5. P = (5*5)/(6*6) = 25/36 Б) m = 1. Лишь одна пара (6;6) удовлетворяет условию. P = 1/(6*6) = 1/36. В) Удовлетворяет условию следующие исходы: (6,4),(4,6),(5,5), (6,5), (5,6), (6,6). m = 6. P = 6/(6*6) = 1/6. Г) Искомому значению удовлетворяет событие, противоположное предыдущему (В), поэтому ответом будет P = 1 - (1/6) = 5/6. Пояснение к Г) : События В) и Г) взаимно противоположные, т.е. они не пересекаются и в объединении дают все пространство исходов, так что P_в + P_г = 1.
догадываюсь, что макс. площадь при определённом периметре будет у квадрата.
докажем это:
обозначим стороны нашего прямоугольника как x и y
периметр его равен 2*x + 2*y = 100м
площадь S = x*y должна быть максимальной
выразим y из уравнения периметра: y = (100 - 2*x)/2 = 50 - x
подставим вместо y в формулу площади: S = x*(50 - x)
S = -x^2+50*x
График функции S=f(x) -это парабола с ветвями, идущими вниз (т.к коэффициент при x^2 -отрицательный). Значит, максимум - это вершина параболы.
Вершина параболы лежит в точке с координатами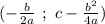
Нам нужна только координата по оси x
x = -50/(2*(-1)) = 50/2 =25м
вторая сторона участка равна: y = 50 - 25 = 25м
ответ: это квадратный участок 25*25метров