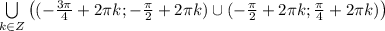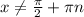
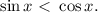
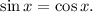Обчислити значення виразу√8 +2 √7 - √8 - 2 √7 - id446066520200117 от fomenko6 17.01.2020 20:55

Question

Алгебра: Обчислити значення виразу√8 +2 √7 - √8 - 2 √7

fomenko6 · Accepted Answer

Знаменатель положителен, поэтому его можно отбросить. Влияет на ответ он только по причине того, что тангенс не всюду определен. Итак, из-за знаменателя $x\not= \frac{\pi}{2}+\pi n$

Отбрасывая знаменатель получаем неравенство $\sin x\ \textless \ \cos x.$

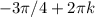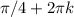Чтобы решить это неравенство, решим сначала уравнение $\sin x=\cos x.$ Решать его можно, деля на косинус и получая при этом уравнение относительно тангенса. Но проще вспомнить, что косинус и синус - это абсцисса и ордината точки на единичной окружности. Они равны на биссектрисе 1-го и 3-го координатных углов. Меньше же ордината будет ниже этой прямой,чему соответствуют промежутки от $-3\pi/4+2\pi k$ до $\pi/4+2\pi k$ .

Выбрасывая x, не попавшие в ОДЗ, получаем объединение интервалов

$\bigcup\limits_{k\in Z}\left((-\frac{3\pi}{4}+2\pi k;-\frac{\pi}{2}+2\pi k)\cup(-\frac{\pi}{2}+2\pi k;\frac{\pi}{4}+2\pi k)\right)$

Обчислити значення виразу√8 +2 √7 - √8 - 2 √7

MOGZ ответил