x1 = -re(acos(-3)) + 2*pi - i*im(acos(-3))
x2 = 2*pi - i*im(acos(4))
x3 = re(acos(-3)) + i*im(acos(-3))
x4 = re(acos(4)) + i*im(acos(4))
Объяснение:
x1 = -re(acos(-3)) + 2*pi - i*im(acos(-3))
x2 = 2*pi - i*im(acos(4))
x3 = re(acos(-3)) + i*im(acos(-3))
x4 = re(acos(4)) + i*im(acos(4))
x1 = 3.14159265358979 + 1.76274717403909*i
x2 = 6.28318530717959 - 2.06343706889556*i
x3 = 3.14159265358979 - 1.76274717403909*i
x4 = 2.06343706889556*i
сумма
-re(acos(-3)) + 2*pi - i*im(acos(-3)) + 2*pi - i*im(acos(4)) + i*im(acos(-3)) + re(acos(-3)) + i*im(acos(4)) + re(acos(4))
=
4*pi + re(acos(4))
произведение
(((-re(acos(-3)) + 2*pi - i*im(acos(-3)))*(2*pi - i*im(acos(4*(i*im(acos(-3)) + re(acos(-3*(i*im(acos(4)) + re(acos(4)))
=
-(2*pi - i*im(acos(4)))*(i*im(acos(-3)) + re(acos(-3)))*(i*im(acos(4)) + re(acos(4)))*(-2*pi + i*im(acos(-3)) + re(acos(-3)))
ответ: 157,5° .
Будем отсчитывать градусы от точки в 12 часов по часовой стрелке. Тогда 15 минут (1/4 часа) у минутной стрелки будут соответствовать (1/4)*360°=90°.
А часовая стрелка за это время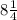 
часа (ведь 15 мин = 1/4 ч и 20 часов - это 8 часов на циферблате), что соответствует 
(8,25 ч умножаем на 30°, потому что 1 час на циферблате - это 360°:12=30°).
Теперь найдем разницу: 247,5° - 90° = 157,5° (этот угол действительно меньший, так как 157,5° меньше 180°, половины всего циферблата).
Задача решена!
X = 2,5
2,5K = - 5
K = - 2
KX = 7
- 2X = 7
X = - 3,5
ОТВЕТ 2) - 3,5