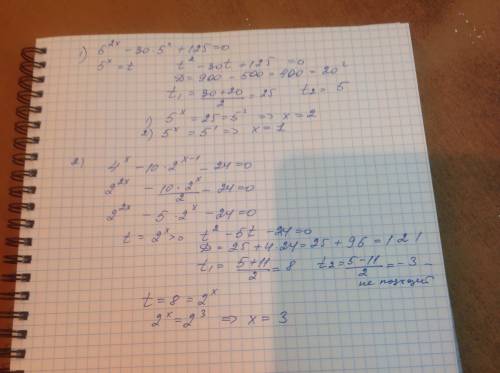
сos(4arctgx)=1/2
4arctgx=±arccos(1/2)+2πn, n∈Z;
4arctgx=±π/3+2πn, n∈Z;
arctgx=±π/12+πn/2, n∈Z;
x=tg(±π/12+πn/2), n∈Z;
cos((±π/12+πn/2))≠0
Поскольку арктангенс - это угол из (-π/2;π/2), при n =0 получим два ответа х=tg(±π/12).
tg(π/12)=(tg(π/4-π/6))=(1 -√3/3)/ (1+√3/3)=
(3-√3)/(3+√3) = (3-√3)²/(3²-(√3)² ) =(12-2√3)/(9-3)=2-√3/3
tg(-π/12)=-tg(π/12)=-(2-√3/3)=-2+√3/3
При n=1 х=tg(±π/12+π/2), указанному промежутку удовлетворяет tg(5π/12)=(tg(π/4+π/6))=(1 +√3/3)/ (1-√3/3)=
(3+√3)/(3-√3) = (3+√3)²/(3²-(√3)² ) =(12+2√3)/(9-3)=2+√3/3
При n=-1 х=tg(±π/12-π/2), указанному промежутку удовлетворяет tg(-5π/12)=-tg5π/12=-(2+√3/3 )=-2-√3/3
При n=2 х=tg(±π/12+π); и при n=-2 х=tg(±π/12-π), Корней нет. Остальные можно не проверять, они не войдут в промежуток
(-π/2;π/2).
ответ. х=±(2-√3/3); х=±(2+√3/3 )
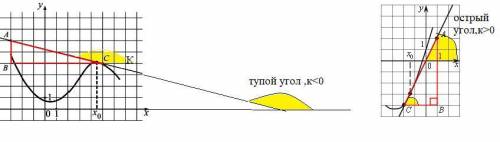
На рисунке изображены график функции и касательная к нему в точке с абсциссой x₀ Найдите значение производной функции в точке x₀
Как понять когда нужно перед значением ставить минус а когда нет??? Только этот вопрос волнует. как пример выложил фото, почему тут с минусом?
Объяснение:
1)Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси ох.
При построении касательной нужно выбирать точки с целочисленными значениями . Например, A (−3; 6), B (−3; 4), C (5; 4). Если касательная составляет с положительным направлением оси ох тупой угол, значит к<0
Угол наклона касательной к оси абсцисс будет равен углу, смежному с углом ACB:
∠ АСК=180- ∠АСВ .
Ищем f ’(x₀) =к= tg ∠АСК = tg(180- ∠АСВ )=- tg∠АСВ =-АВ/ВС=-2/8=-0,25.
2) Выбираем точки с целочисленными значениями A (1; 2), B (1; −4), C(−2; −4). Угол наклона касательной к оси абсцисс будет равен ∠ACB:
f ’(x₀) =к= tg ∠АСВ =АВ/ВС=6/3=2.
Понятнее? Чертеж твой весь черный. Прикрепила другой.