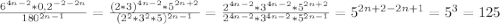
Надеюсь,что это правильный ответ..
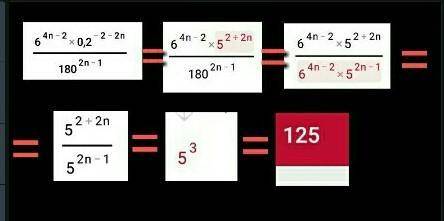
1. < var > x^3y^34z^22y=8x^3y^4x^2 < /var ><var>x3y34z22y=8x3y4x2</var>
2. < var > -2x^60,5x^2y^3=-x^8y^3 < /var ><var>−2x60,5x2y3=−x8y3</var>
3. < var > (-5z^2y^3)^3=-125z^6y^9 < /var ><var>(−5z2y3)3=−125z6y9</var>
4. < var > -0,03ab^3=-0,03*(-4)*(-2)^3=0.96 < /var ><var>−0,03ab3=−0,03∗(−4)∗(−2)3=0.96</var>
5. < var > (18a^3b^2c)(\frac{1}{6}ab^3c^2)(-\frac{1}{3}a^2bc^3)=-a^6b^6c^6 < /var ><var>(18a3b2c)(61ab3c2)(−31a2bc3)=−a6b6c6</var>
Объяснение:
Рад
x2 + 4x + 8 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 42 - 4·1·8 = 16 - 32 = -16
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
4x2 - 12x + 9 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-12)2 - 4·4·9 = 144 - 144 = 0
Так как дискриминант равен нулю то, квадратное уравнение имеет один действительных корень:
x = 122·4 = 1.5
3x2 - 4x - 1 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-4)2 - 4·3·(-1) = 16 + 12 = 28
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 4 - √282·3 = 23 - 13√7 ≈ -0.21525043702153024
x2 = 4 + √282·3 = 23 + 13√7 ≈ 1.5485837703548635
2x2 - 9x + 15 = 0 Найдем дискриминант квадратного уравнения: D = b2 - 4ac = (-9)2 - 4·2·15 = 81 - 120 = -39 Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.