Воспользуемся методом неопределенных коэффициентов
А В А * (Х + 6) + В * (Х - 6) (А + В) * Х + (6 * А - 6 * В) Х + 28
+ = = =
Х - 6 Х + 6 (Х - 6) * (Х + 6) Х² - 36 Х² - 36
Приравнивая коєффициенты при подобных членах получаем систему линейных уравнений
А + В = 1 А = 17/6
6 * А - 6 * В = 28 , откуда B = -11/6
Таким образом
Х + 28 17/6 11/6
= -
Х² - 36 Х - 6 Х + 6 неуверен с моим номером пож
Для того чтобы найти промежутки возрастания и убывания необходимо взять производну от даннйо функции и решить следующие неравенства
y'(x)<0 при х удовлетворяющих этому неравнетсву функция убывает
y'(x)>0 при х удовлетворяющих этому неравенству функция возрастает
Найдем y'(x)=(0.5cos(x)-2)'=-0.5sin(x)
Теперь решим неравенство:
-0.5sin(x)<0 или оно эквивалентно следующему неравенству:
sin(x)>0
Это неравенство имеет решения при 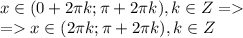
Значит на этих интервалах функция убывает.
Теперь рассмотри неравенство -0.5sin(x)>0 оно эквивалентно неравенству:
sin(x)<0
И имеет следующие решения: 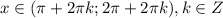
Значит на этих интервалах функция возрастает.
На границах интервалов функция имеет точку перегиба.
Функция y=0,5cos(x)-2 возрастает при 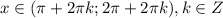
Убывает при 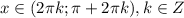
И имеет точки перегиба при 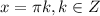
х = (-2 -4)/2 = -3
у = (-1 +3)/2 = 1
К(-3; 1) - центр окружности
Найдём длину MN - это будет диаметр ( разделим на 2 , получим радиус)
MN = √(-4 +2)² + (3 +1)² = √20 = 2√5 ⇒R = √5
Уравнение окружности в общем виде (х - х0)² + (у - у0)² = R²
В нашем случае: (х +3)² + (у -1)² = 5