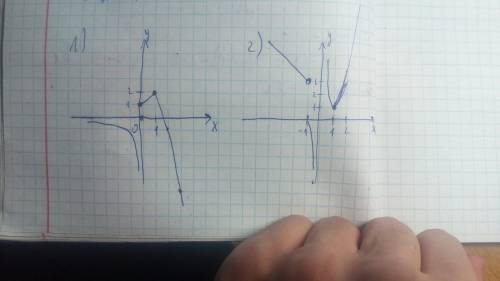
1) для того чтобы функция была непрерывной, нужно чтобы пределы слева и справа в точках 0 и 1 были равны. Найдем их:
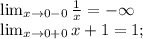
Так как 1≠-∞, то точка 0- это точка разрыва(второго рода).
Чтобы функция была неразрывной в точке 1, нужно чтобы предел от 3-ax^2 был равен 2, так как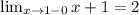 
При x=1 ⇒y=2.
Подставим координаты (1;2) в формулу y=3-ax^2⇒2=3-а⇒а=1, то есть уравнение имеет вид y=3-x^2. Проверим это: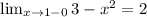 
Действительно 2=2, значит функция не будет являться непрерывной в точке 1.
ответ: х=0 - точка разрыва. функция непрерывна в точке х=1 при а=1
2) Аналогично:
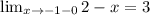
3≠-1, значит -1- это точка разрыва.
В точке x=1 ⇒y=1. Подставим: 1=a*1⇒a=1.
Проверим: 
.
Так как точка х=0 лежит в области определения функции 
, а из ОДЗ следует что х≠0, то функция также будет прерываться в точке х=0
ответ: х=-1 - точка разрыва, х=0- точка разрыва, функция будет непрерывна в точке х=1 при а=1
Ни четная ни нечетная(функция общего вида)
Объяснение:
1) Область определения - вся числовая прямая, это значит, что этот параметр не влияет на четность(функция может быть как четной, так и нечетной, так и общего вида)
2) Функция четна, если f(-x) = f(x), проверяем, f(-x) = 5 + 3x^3 и это не равно f(x), значит функция не может быть четной
3) Функция нечетна, если f(-x) = -f(x), проверяем, f(-x) = 5 + 3x^3 и это не равно -f(x), значит функция не может быть нечетной
4) Таким образом, эта функция ни четная ни нечетная, т.е. эта функция общего вида
Обозначим за x знаменатель дроби, тогда числитель будет равен x-14;
Теперь рассмотрим обратную дробь:
Знаменатель будет равен (x-14)+33, а числитель x-9;
Составим уравнение:
(x-14)/x=((x-14)+33)/(x-9);
(x-14)/x=(x+19)/(x-9);
x^2-9x-14x+126=x^2+19x;
126=42x;
x=3;
Значит, числитель будет равен: x-14=3-14=-11.
Дробь: -3/11.
Сделаем проверку подставив значение икса во второе условие:
Числитель: x-9=3-9=-6;
Знаменатель: (3-14)+33=22
Дробь: -22/6=-11/3, что соответствует обратной нашей дроби.