Произведение чисел, переменных и их степеней называется одночленом, например, 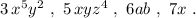
Одночлены можно сложить с приведением подобных членов в случае, если буквенная часть одинакова, а коэффициенты (числовые множители перед буквенной частью ) различные.
Действуем по правилу сложения подобных слагаемых. Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Например, из того, что написано:
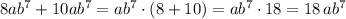 ,
,
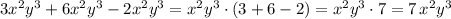 .
.
Если одночлены не подобны, то упрощение суммы не получится, а останется многочлен, то есть сумма нескольких одночленов. Например, сумма одночленов
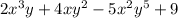 не может быть упрощена, так как буквенные части одночленов различны.
не может быть упрощена, так как буквенные части одночленов различны.
А вот пример, где можно немного упростить сумму одночленов, но в результате всё равно получим многочлен:
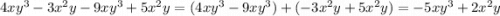 .
.
Одночлены можно сложить с приведением подобных членов в случае, если буквенная часть одинакова, а коэффициенты (числовые множители перед буквенной частью ) различные.
Действуем по правилу сложения подобных слагаемых. Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Например, из того, что написано:
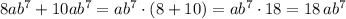 ,
,
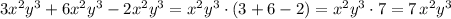 .
.
Если одночлены не подобны, то упрощение суммы не получится, а останется многочлен, то есть сумма нескольких одночленов. Например, сумма одночленов
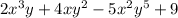 не может быть упрощена, так как буквенные части одночленов различны.
не может быть упрощена, так как буквенные части одночленов различны.
А вот пример, где можно немного упростить сумму одночленов.
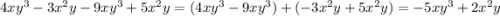 .
.
2 смена - 40% от оставшихся
3 смена - ?
Составляем пропорцию:
210 - это 30%
х - это 100%
Находим х: х=210*100/30=700 (человек)
2) 700-210=490 - остальные дети
Т.к. сказано, что 40% от остальных детей, находим эти 40% также с пропорции:
490 - это 100%
х(1) - это 40%
х(1)=490*40/100=196 (человек)
3) Находим число детей, принятых в 3 смену:
700-(196+210) = 294 (человека)
ответ: 294
Надеюсь, правильно :)