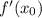производная функции в данной точке. А 
точка касания по иксу.
мы должны найти производную общего типа этой функции.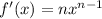
- где n это степень.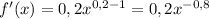
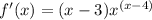
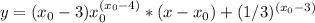
и получаешь уравнение касательной.
Учебно-методическое пособие для подготовки школьников к экзаменам, разработанное в Учебном центре "Резольвента". В пособии рассмотрены следующие во Решение рациональных уравнений; 2. Область определения рационального уравнения; 3. Решение иррациональных уравнений; 4. Область определения иррационального уравнения; 5. Рациональные уравнения, сводящиеся к квадратным при замены переменной; 6. Иррациональные уравнения, сводящиеся к квадратным при замены переменной; 7. Метод уединения радикала. Приведены примеры решения задач и задачи для самостоятельного решения. <a href="http://window.edu.ru/window/library?p_mode=1&p_qprovider=314&p_rubr=2.1.11" target="_blank">Пособия Учебного центра "Резольвента" для подготовки к ЕГЭ и ГИА по математике ->></a>
