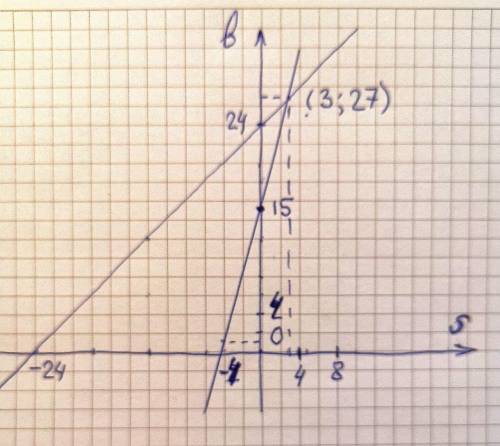
(3,27)
Объяснение:
Переводим условие в алгебраическую форму
s - возраст сына, b - возраст батька
s + 24 = b
4(s +5) = b + 5
упростим второе уравнение
4s +20 - 5 = b
4s + 15 = b
Осталось решить систему графическим образом. Лучше бы на миллиметровке, но если ее нет, то можно взять клетки в масштабе 1 - это полклетки.
График первого уравнения (прямую) построим по точкам:
s = 0 ; b =24
s = -24 ; b = 0
График второго уравнения (прямую) построим по точкам:
s = -4; b = 1
s = 0 ; b = 15
Прямые пересеклись в точке (3;27), то есть s = 3 это возраст сына, а b = 27 - возраст батька.
В решении.
Объяснение:
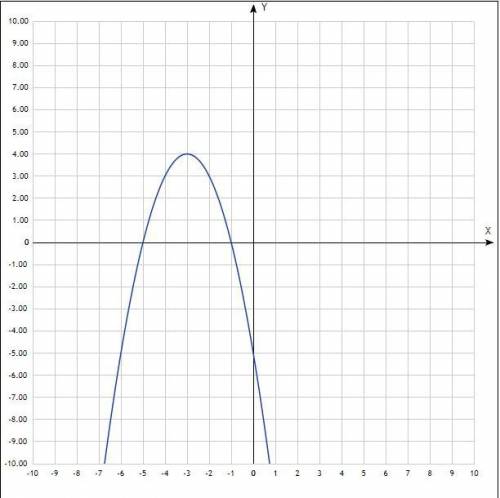
Функцію задано формулою f(x)= -x² - 6x - 5.
1) Знайдіть проміжок спадання функції f(x).
Квадратичная функция, график - парабола, ветви направлены вниз.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу, построить график.
Таблица:
х -7 -6 -5 -4 -3 -2 -1 0 1
у -12 -5 0 3 4 3 0 -5 -12
Согласно графика, функция убывает при х∈(-3; +∞).
2) Розв'яжіть нерівність -х²-6х>5.
-х² - 6х > 5
-х² - 6х - 5 > 0
Приравнять к нулю и решить квадратное уравнение:
-х² - 6х - 5 = 0/-1
х² + 6х + 5 = 0
D=b²-4ac =36 - 20 = 16 √D=4
х₁=(-b-√D)/2a
х₁=(-6-4)/2
х₁= -10/2
х₁= -5;
х₂=(-b+√D)/2a
х₂=(-6+4)/2
х₂= -2/2
х₂= -1.
Уравнение квадратичной функции, график - парабола, ветви направлены вниз, пересекают ось Ох в точках х= -5 и х= -1.
Решение неравенства: х∈(-5; -1).
Неравенство строгое, скобки круглые.
Делители числа 6:
ответ: (1; 7); (0; -5); (2; 3); (-1; -1)