Из верхнего выражения выражаем x=4y-1.
Подставим это во второе выражение, получим: 2y*(4y-1)=1
Умножаем, получаем систему:
х=4у-1
{
8y^2 - 2y - 1=0
Рассматриваем второе уравнение. (Решаем через дискриминант). Д=4+4*8*1=36
y1=(2-6)/16= -1/4
y2= (2+6)/16=1/2
Теперь, 2 случая значений у подставляем в наше "х=4у-1", получаем что:
х1= -2
х2= 1
ответ: (-2 ; -1/4) ; (1 ; 1/2)
1) 6 км/ч; 2) 27 км/ч
Объяснение:
Пусть х - собственная скорость катера
х + 3 - скорость катера по течению реки
х - 3 - скорость катера против течения реки
По условию
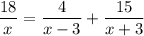
18(x² - 9) = 4x(x + 3) + 15x(x-3)
18x² - 162 = 4x² + 12x + 15x² - 45x
x² - 33x + 162 = 0
D = 33² - 4 · 162 = 441 = 21²
x₁ = 0.5 (33 -21) = 6 (км/ч)
х₂ = 0,5 (33 + 21) = 27 (км/ч)
По смыслу задачи и то и другое число подходит. Проверим.
1) 6 км/ч
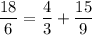
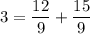
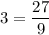
3 ≡ 3 (верно!)
2) 27 км/ч
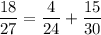
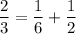
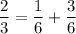
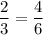
2/3 ≡ 2/3 (всё верно)
При движении с собственной скоростью 6км/ч путь займет у катера 3 часа, а при движении со скоростью 27 км/ч путь займёт 2/3 ч = 40 мин.
27 км/год
6 км/год
Объяснение:
Возьмем за x - власну швидкість
Проти течії: S = 4 ; V = x - Vтеч; T= Tпр.т.
За течією: S = 15 ; V = x + Vтеч; T= Tза.т.
Без течії: S=18; V=x; T= Tпр.т.+Tза.т.
Формулы: S=V*T; V=S/T; T=S/V
Tпр.т.= 4/(x - Vтеч), за умовою: Vтеч = 3 км/год.
Tпр.т.= 4/(x - 3)
Tза.т.=15/(x+3)
T(без течії)=18/x, а також:
T(без течії)=Tпр.т.+Tза.т
Тому можемо зробити рівняння:
Tпр.т.+Tза.т=18/x
4/(x - 3) + 15/(x+3) = 18/x
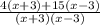=18/x
(4x+12+15x-45)x = 18(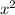
- 9)
19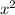-33x-18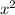+152=0
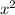-33x+162=0
D=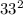
-4*162=441
x1=(33+21)/2=27 км/год
x2=(33-21)/2=6 км/год
4y-x=1
2xy=1
x=4y-1
2xy=1
x=4y-1
2(4y-1)y=1
x=4y-1
8y^2-2y-1=0 |:8
x=4y-1
y^2-y/4-1/8=0
y^2-y/4-1/8=0
y1=1/2
y2=-1/4
x1=4*(1/2)-1
y1=1/2
x2=4*(-1/4)-1
y2=-1/4
x1=1
y1=1/2
x2=-2
y2=-1/4
ответ: (1;-1/2) и (-2;-1/4).