1) 1-3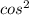
x=2sin(x)cos(x)
единицу представим по тригонометрическому тождеству:1=sin²x+cos²x
sin²x+cos²x-3cos²x-2sin(x)cos(x)=0
sin²x-2sin(x)cos(x)-2cos²x=0
делим каждый член уравнения на cos²x
tg²x-2tgx-2=0
решаем квадратное уравнение
D=12
tgx₁=1+√3 tgx₂=1-√3
x₁=arctg(1+√3)+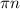
x₂=arctg(1-√3)+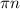
2) 3Sin²x+2SinxCosx=2
3Sin²x+2SinxCosx=2(Sin²x+Cos²x)
Sin²x+2SinxCosx-2Cos²x=0
Уравнение однородное 2 степени. Разделим его на Cos²x
Tg²x+2Tgx-2=0
Tgx=y
y²+2y-2=0
D=12>0
y=(-2+2√3)/2=-1+√3 или y=(-2-2√3)/2= -1-√3
Tgx=-1+√3⇒ x=arctg(-1+√3)+πn,n∈Z
Tgx= -1-√3 ⇒x= arctg(-1-√3)+πn,n∈Z
Обратившись к основному тригонометрическому тождеству, получим:
2sin^2(x) - 5sin(x)cos(x) + 5cos^2(x) = sin^2(x) + cos^2(x);
sin^2(x) - 5sin(x)cos(x) + 4cos^(x) = 0.
Разделим полученное уравнение на cos^2(x):
tg^2(x) - 5tg(x) + 4 = 0.
Произведем замену переменных t = tg(t):
t^2 - 5t + 4 = 0.
Корни квадратного уравнения вида ax^2 + bx + c = 0 определяются
по формуле: x12 = (-b +- √(b^2 - 4 * a * c) / 2 * a.
t12 = (5 +- 3) / 2;
t1 = 1; t2 = 4.
tg(x) = 1;
x1 = π/4 +- π * n.
x2 = arctg(4) +- π * n.
Объяснение:
d=-4.6
an=a1+(n-1)d
an=96.4+(n-1)(-4.6)=96.4-46n+4.6=101-4.6n
101-4.6n>=0
4.6n>=101
n=22
22 положительных