№1.
Если трехчлен (2х²- 7х+а) содержит множитель ( х - 4), значит один из корней уравнения 2х²- 7х+а= 0 равен 4, т.е. х=4
Подставим х=4 в уравнение 2х²- 7х+а=0 и найдем а.
2·4²- 7·4+а =0
а=28-32
а= - 4
№2.
4х²+ ах + 6 содержит множитель ( 2х + 1)
1)2х+1=0
х= - 0,5 - это первый корень уравнения 4х²+ах+6=0
2) Делим обе части уравнения 4х²+ах+6=0 на 4 и получим приведенное квадратное уравнение:
х²+0,25ах+1,5=0
3) По теореме Виета для приведенного квадратного уравнения найдем второй корень,
х₁ * х₂ = 1,5
х₂=1,5 : (-0,5)
х₂= - 3
4) По теореме Виета для приведенного квадратного уравнения найдем второй коэффициент, стоящий при х.
х₁+х₂= -0,25а
- 0,25а = - 0,5 + (-3)
- 0,25а = - 3,5
а = - 3,5 : (-0,25)
а = 14
у(наиб) = 32 ( в точке х=2)
у(наим) = 5 ( в точке х=1)
На границах интервала.
Объяснение:
Для того, чтобы найти наибольшее и наименьшее значение функции нам необходимо:
Найти все стационарные точки.Найти все критические точки. Проверить границы интервала. Пункт 1 - стационарные точки:Данные точки ищутся с производной. Найдем производную данной функции:
x'(t) = 8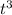
- 3.
Приравниваем производную к 0:
8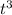 - 3 = 0
t = ±![\sqrt[3]{\frac{3}{8} }](/tpl/images/1201/0058/69c06.png)
= ±![\frac{\sqrt[3]{3} }{2}](/tpl/images/1201/0058/4c079.png)
- однако, эти точки не входят в наш интервал.
Таковых у нас нет, т.к. критические точки - это стационарные точки, но которые не входят в ОДЗ. (У нас ОДЗ от (-∞;∞+)).
Пункт 3 - границы графика:Подставляем значения границ интервала и находим значения в этих точках:
x(1)=2*1^4−3*1+6 = 5
x(2)=2*2^4−3*2+6 = 32
Следовательно, это и есть наибольшее и наименьшее значение функции на заданном интервале.
Там как при m в пределах от минус шести до шести дискриминант будет отрицательным, что обозначает отсутствие действительных корней, а при значения -6 и 6 решение будет одно