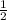* √196+1,5*√0,36= 0,5*14+1,5*0,6=7,9
Запишем уравнение кривой в виде -4*(x²-4*x)+25*(y²+4*y)-16=0, или -4*[(x-2)²-4]+25*[(y+2)²-4]-16=0, или -4*(x-2)²+25*(y+2)²=100, или -(x-2)²/25+(y+2)²/4=1. Это есть уравнение гиперболы с центром симметрии в точке (2;-2), вещественной полуосью a=√25=5 и мнимой полуосью b=√4=2. Вершины гиперболы в данном случае лежат на прямой x=2, параллельной оси ординат. Одни из вершин имеет координаты (2;3), другая - координаты (2;-7). Асимптоты гиперболы задаются уравнениями y-y0=b/a*(x-x0) и y-y0=-b/a*(x-x0), где x0 и y0 - координаты центра симметрии. В нашем случае x0=2, y0=-2, a=5,b=2, поэтому уравнения асимптот принимают вид: y+2=2/5*(x-2) и y+2=-2/5*(x-2).
корень из 0,36 это 0,6
Получается,
1/2*14+1,5*0,6=7+0,9=7,9