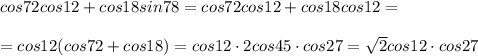
1)Уравнение прямой будем искать в виде y = kx + b, надо найти k и b. Этим мы и займёмся.
Прямая проходит через начало координат, это говрит о том, что речь идёт не о линейной функции, а о её частном случае - прямой пропорциональности, задаваемой формулой y = kx. Теперь совсем элементарно найти k. Подставив координаты другой точки в y = kx, найдём отсюда k:
-3 = 4k
k = -3/4
Таким образом, уравнение данной прямой такое - y = -3/4x
2)Этот случай немного сложнее предыдущего. Общий вид прямой опят y = kx + b. Воспользуемся здесь тем, что прямая проходит через данные точки, тогда её координаты, по логике вещей, должны удовлетворять данному уравнению. Подставим в него координаты обеих точек, и решим полученную систему уравнений с двумя переменными:
-3k + b = 4 -3k + b = 4 -2k = 6 k = -3
-k + b = -2 k - b = 2 b - k = -2 b = -5
Всё, коэффициенты найдены. Искомое уравнение прямой - y = -3x - 5
Объяснение:
1. 1)3x²-27=0;
3(x²-9)=0; 3≠0;
x²-9=0;
x²=9;
x=√9=±3.
***
2) x²-16=0;
x²=16;
x=√16=±4.
***
3) 2x²=8;
x²=4;
x=√4=±2;
***
4) 4x²+1=0;
4x²= -1;
x²= - 1/4 - корня нет - х² должен быть положительным.
***
5) x²+1=0;
x²=-1 - корня нет - х² должен быть положительным.
***
6) x²-6x=0;
x(x-6)=0.
x1=0;
x-6=0;
x2=6.
***
7) x²+2x=0;
x(x+2)=0;
x1=0;
x+2=0;
x2= -2.
***
8) x²-8x=0;
x(x-8)=0;
x1=0;
x-8=0;
x2=8.
***
9) x²-7x=0;
x(x-7)=0;
x1=0;
x-7=0;
x2=7.
***
10) x²+3x=0;
x(x+3)=0;
x1=0;
x+3=0;
x2= -3.
2. 1) x²-5x-7=0;
a=1, b=-5, c=-7;
D=b²-4ac=(-5)²-4*1*(-7)=25+28=53;
D=53 - два корня.
***
2) x²+6x+10=0;
a=1, b=6, c=10;
D=6²-4*1*10=36-40=-4.
D= -4, нет корней.
***
3) x²-4x+7=0;
a=1, b=-4, c=7;
D=(-4)²-4*1*7=16-28= -12;
D= -12 - нет корней.
***
4) x²-10x+25=0;
a=1, b=-10, c=25;
D=(-10)²-4*1*25=100-100=0;
D=0 - два равных корня x1=x2.
***
5) x²-8x+2=0;
a=1, b=-8, c=2;
D=(-8)²-4*1*2=64-8=56;
D=56 - два корня.
***
6) x²-9x+1=0;
a=1, b=-9, c=1;
D=(-9)²-4*1*1=81-4=77;
D=77 - два корня.
***
7) x²-x+9=0;
a=1, b=-1, c=9;
D=(-1)²-4*1*9=1-36= -35;
D= -35 - нет корней.
***
8) x²-6x-4=0;
a=1, b=-6, c=-4;
D=(-6)²-4*1*(-4)=36+16=52;
D=52 - два корня.
***
9) x²-14x+49=0;
a=1, b=-14, c=49;
D=(-14)²-4*1*49=196-196=0;
D=0 - два равных корня.
***
10) x²-4x+x=0;
a=1, b=-4, c=4;
D=(-4)²-4*1*4=16-16=0;
D=0 - два равных корня.