если только одну, то
например
3) Решите уравнение: 1-5-11-...-х=-207
-5-11-...-х=-207-1=-208
5+11+...+x=208
5, 11, это арифметическая прогрессия с первым членом 5 и разницей 11-5=6 арифметической прогрессии
и последним членом -x
5+11+...+x=208
сумма прогрессии по формуле
S=(a[1]+a[n])/2*n
n=(a[n]-a[1])/d+1
n=(x-5)/6+1
(5+x)/2*((x-5)/6+1)=208
(x+5)(x-5+6)=208*2*6
(x+5)(x+1)=2496
x^2+6x+5-2496=0
x^2+6x-2491=0
D=100^2
x1=(-6-100)/2<0 - очевидно не подходит, так х положительное целое
х2=(-6+100)/2=47
ответ 47
главная идея задачи - использование арифметической прогрессии и ее свойств
ну и по ходу уметьрешать квадратное уравнение
Сначала мы пишем систему и смотрим на коэффициенты при х и у.
В данном случае, особой разницы нет, поэтому останавливаемся на коэффициентах при х. В первом уравнении коэффициент при х равен 4, а во втором 3. Нам надо, чтобы при почленном сложении двух уравнений сумма коэффициентов при х равнялась нулю. Этого можно добиться искусственно, если первое уравнение домножить на 3, а второе уравнение домножить на (-4) (данная операция обозначена вертикальными "палочками", после которых стоит знак умножения на нужное нам число
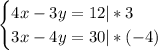
Получаем следующую систему:
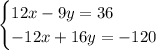
Теперь складываем уравнения "почленно", т.е. иксы с иксами, игреки с игреками, свободные члены со свободными членами. В результате получаем:
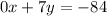
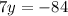
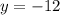
Осталось найти х. Для этого найденное значение у=-12 подставим в любое из первоначальных уравнений, например, в первое:
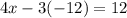

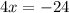

Осталось записать ответ. Допускаются следующие записи:
х=-6, у=-12 или (-6;-12)
Решаем уравнение x^2-5*x-6=0:
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-5)^2-4*1*(-6)=25-4*(-6)=25-(-4*6)=25-(-24)=25+24=49;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√49-(-5))/(2*1)=(7-(-5))/2=(7+5)/2=12/2=6;
x_2=(-√49-(-5))/(2*1)=(-7-(-5))/2=(-7+5)/2=-2/2=-1.
Поэтому x^2-5*x-6 = (х - 6)(х + 1).
Выражение: x^2-8*x+16 это квадрат выражения :
x^2-8*x+16=(х - 4)².
Исходное выражение преобразовано в такое:
Последнее выражение всегда положительно (оно в квадрате).
Кроме значения х = 4. При этом всё выражение превращается в 0.
Значит, решает всё первая часть - кубический корень из произведения.
Меньше нуля (то есть отрицательным) корень кубический может быть при отрицательном значении подкоренного выражения.
Произведение (х - 6)(х + 1) может быть отрицательным при (-1 < x < 6).
С учётом того, что из этого промежутка для всего выражения выпадает значение х = 4, то ответ:
(-1< x < 4). (4 < x < 6).
Вот конкретные значения заданного неравенства в полученном промежутке:
-2 -1 0 1 2 3 4 5 6 7
72 0 -29.074 -19.390 -9.158 -2.289 0 -1.817 0 18