Периметр прямоугольника равен : (а + в) * 2 , где а и в - стороны прямоугольника . Площадь прямоугольника равна : S = а * в . Из условия задачи имеем (а + в) * 2 = 26 см ; а + в = 13 ; а = (13 - в) S = (13 - в) * в = 36 ; 13в - в^2 = 36 ; в^2 - 13в + 36 = 0 D = (- 13)^ - 4 * 1 *36 = 169 - 144 = 25 ; Sqrt(25) = 5 Найдем корни уравнения . в' = (-(- 13) + 5) / 2*1 = (13 + 5) / 2 = 9 ; в" = (- (- 13) - 5) / 2 * 1 = (13 - 5) / 2 = 4 . Получили 2 действительных корня : 9 см и 4 см . Другая сторона прямоугольника будет соответственно равна : 4 см и 9см
2x²+7x-9=0
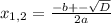
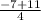 =
=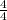 =1
=1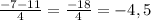
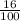
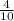
D=b²-4ac=7²+4*2*9=49+72=121=11²
x₁=
x₂=
100x²-16=0
100x²=16
x²=
x₁,₂=±
3x²=18x
3x²-18x=0
x(3x-18)=0
x=0 3x-18=0
3x=18
x=6
x²-16x+63=0
D=b²-4ac=(-16)²-4*63=256-252=4=2²
x_{1,2}= \frac{-b+-\sqrt{D}}{2a}[/tex]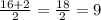
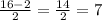
x₁=
x₂=