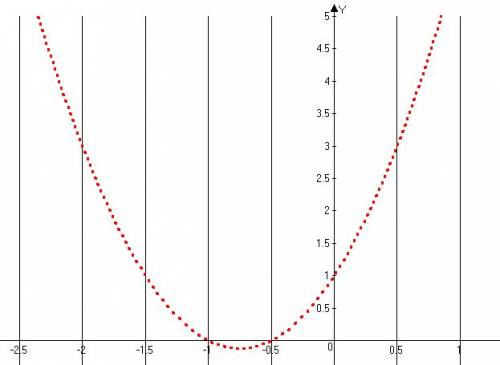
X(-2)⇒Y(3)
X(-1)⇒Y(0)
X(0)⇒Y(1)
X(1)⇒Y(6)
=================================
см.рис
1) б
bn+1 = bn * q
q = b2\ b1 = -4\-2 = 2
q = 2
b1 = -2
b2 = -4
b3 = -8
b4 = -8 * 2 = -16
b5 = -16 * 2 = -32
b6 = -32 * 2 = -64
b7 = -64 * 2 = -128
b 8 = -128 * 2 = -256
b9 = -256 * 2 = -512
Sn = b1 (q^n−1) \ q−1
S9 = -2( 2^9-1) \ 2 - 1
S9 = -1022
1) x1 = 8; x2 = 2
2) x1 = 3; x2 = -1
3) x = 2/3
Объяснение:
1) -x^2 + 10x - 16 = 0 (*(-1))
x^2 - 10x + 16 = 0
по т. Виета
x1 + x2 = 10 x1 = 8
x1 * x2 = 16 → x2 = 2
Или через дискриминантD = (-10)^2 - 4 * 1 * 16 = 100 - 64 = 36 (6^2)
x1 = (10+6)/2 = 16/2 = 8
x2 = (10-6)/2 = 4/2 = 2
2) -2x^2 + 4x + 6 = 0 (*(-1))
2x^2 - 4x - 6 = 0
D = (-4)^2 - 4 * 2 * (-6) = 16 + 48 = 64 (8^2)
x1 = (4+8)/2*2 = 12/4 = 3
x2 = (4-8)/2*2 = -4/4 = -1
3) 9x^2 - 12x + 4 = 0
D = (-12)^2 - 4 * 9 * 4 = 144 - 144 = 0
x = 12/2*9 = 12/18 = 2/3
2x2+3x+1=0
Коэффициенты уравнения:
a=2,
b=3,
c=1
Вычислим дискриминант:
D=b2−4ac=32−4·2·1=9−8=1
(D>0), следовательно это квадратное уравнение имеет 2 различных вещественных
корня:
Вычислим корни:
x(1,2)=(−b± √D) / 2a
x1=−b+√D разделить на 2
x1=(−3+1)/2*2=-2/4=-0,5
x2=-b- √D разделить на 2
x2=(−b−√D)/2a=(−3−1)/2*2=-4/4=-1
точки (-0.5;0) и (-1;0)
x1 и x2- точки пересечения с осью Ох
с осью Оу, когда х=0
пишешь квадратное уравнение, без правой части..
2x^2+3x+1=2*0+3*0+1=1
точка(0;1)