а) возьмем третий аквариум за х, тогда первый аквариум 1,5х, а второй х+5, составим уравнение:
1,5х+(х+5)+х=61
1,5х+х+5+х=61
3,5х=61-5
3,5х=56
х=16-третий аквариум
1,5*16=24-первый аквариум
16+5=21-второй аквариум.
б) возьмем 2 пакет за х, тогда первый пакет 1,5х, третий и четвертый 0,5х. составим уравнение:
1,5х+х+х+0,5+х+0,5=14,5
4,5х+1=14,5
4,5х=13,5
х=3-второй пакет
1,5*3=4,5-первый пакет
0,5 +3=3,5третий и четвертый пакет.
1) рассмотрим сначала первый корень:
1.1 распишем синус двойного угла, вынесем 4 за скобки
1.2 единицу распишем по основному тригонометрическому тождеству как 1 = sin²a + cos²a
1.3 в скобках можно собрать формулу (а - б)² = а² + б² - 2аб
1.4 помним о том, что корень извлекается по модулю
1.5 так как по условию дано, что угол находится в 4 четверти, в которой синус отрицательный, а косинус положительный, то раскрываем модуль со знаком плюс
2) рассмотрим второй корень:
2.1 вынесем 2 за скобки и распишем косинус двойного угла
2.2 единицу распишем по основному тригонометрическому тождеству и приведем подобные слагаемые
2.3 корень извлекается по модулю, косинус раскрываем с +
3) переписываем то, что получилось, приводим подобные слагаемые

а) две точки пересечения (два корня)
b)
Объяснение:
a) 
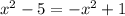 в)
в)  окружность R=3, O(0;0) и
окружность R=3, O(0;0) и

 парабола с ветвями вниз, вершина(0;4)
парабола с ветвями вниз, вершина(0;4)
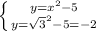 четыре точки симметричные относительно
четыре точки симметричные относительно
 оси "y"
оси "y"
б) xy=3 или 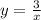 гипербола, точка симметрии (0;0)
гипербола, точка симметрии (0;0)
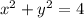 окружность R=2 центр (0,0)
окружность R=2 центр (0,0)
точек пересечения графиков нет, самые близкие точки к началу кординат в точках х=у, у гиперболы 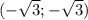 и
и 
у окружности  и
и 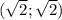
г)  это две окружности: одна R=4, центр (0;0)
это две окружности: одна R=4, центр (0;0)
другая R=2 центр (0;2), точка касания (0;4) одна.
ну а графики придется рисовать по клеткам, используя циркуль и лекала для точности построения. Удачи.
a) x=1,5z, y=z+5. x+y+z=61, 1,5z+z+5+z=61, 3,5z=56, z=16, x=16*1,5=24, y=16+5=21
б) x=1,5y, z=y+0,5, w=y+0,5. x+y+w+z=14,5, 1,5y+y+2(y+0,5)=14,5, 4,5y=13,5, y=3, x=4,5, z=w=3,5