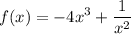
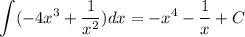

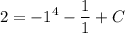
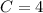

ответ:Т.к. известен один корень уравнения, значит подставив его в выражение, можно найти неизвестный коэффициент q.
3 в квад - 5 * 3 + q = 0,
9 – 15 + q = 0,
q = 15 – 9,
q = 6.
Тогда исходное уравнение будет иметь вид:
х² - 5х + 6 = 0.
Определяем, чему равен дискриминант:
D = b2 - 4ac
D = 25 - 4 * 6 = 25 - 24 = 1.
Находим, чему равны корни квадратного уравнения, которых 2 при положительном дискриминанте.
х = (-b ± √D) / 2a
х = (5 ± 1) / 2
х1 = 2, х2 = 3.
ответ: коэффициент q равен 6, второй корень уравнения равен 2.
Объяснение: