5π/6
Объяснение:
попробуем-ка раскрыть этот зловредный модуль. определим, при каких "хэ" нужно раскрыть его с плюсом, то есть как есть, а при каких с минусом.
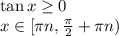
иными словами, мы раскрываем модуль с плюсом, когда икс находится в 1 или 3 четверти.
тогда:
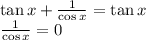
жалко, в этом случае корней нет :(
но не беда! можно же раскрыть модуль с минусом, в этом случае икс бегает во 2 и 4 четвертях.
тогда:
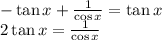
с этого момента следует сказать, что икс не может быть равным π/2 + πn, так как знаменатель обращается в нуль, и тангенс не определен в этой точке (собственно говоря по той же причине)
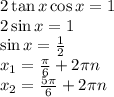
первый корень находится в первой четверти, так что его сразу скидываем в свалку. второй подходит по всем параметрам, наименьший положительный корень будет равен 5π/6 (при n = 0)
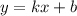общий вид уравнении прямой. Поскольку графики параллельны, то угловые коэффициенты у них совпадают, т.е.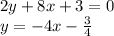 
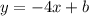(*) . Прямая (*) проходит через точку M(2;3), следовательно, подставив координаты х=2 и у=3 в (*), получим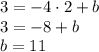 
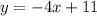- искомая прямая.
5^x ( 1 - 5^(-2)) = 600
5^x ( 1 - 1/25) = 600
5^x ( 25/25 - 1/25) = 600
5^x * 24/25 = 600
5^x = (24*25*25)/24
5^x = 25^2
5^x = (5^2)^2
5^x = 5^4
x = 4