Третье решить не получается, прости
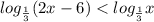
Так как основания логарифмов равны, мы можем их опустить и решать как обычное уравнение
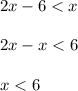
x ∈ ( -∞ ; 6 )
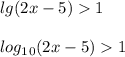
Из единицы нам нужно представить десятичный логарифм , чтобы как в первом уравнении их можно было опустить
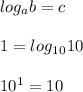
Теперь вместо единицы подставим логарифм
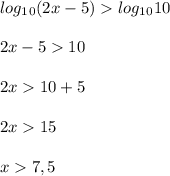
x ∈ ( 7,5 ; +∞ )
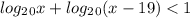
как и в предыдущем неравенстве, единицу представляем в виде логарифма с тем же основанием
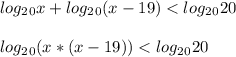
По свойству логарифма ⇒ logₐb + logₐc = logₐ ( b · c )
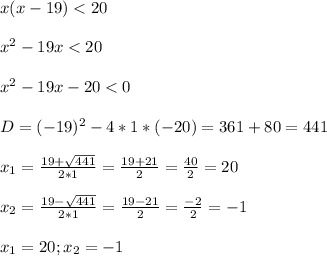
x < 20 ; x < -1
Подставим получившиеся значения в выражение, то есть сделаем проверку ( не всегда оба корня подходят )
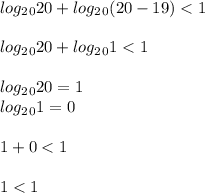
Так как по обе стороны значения получились одинаковыми, можно считать что решение верно ( беря числа меньше 20, неравенство будет верным )
Подставим второй корень
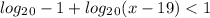
Сразу можно сказать что корень не подходит, так как логарифма отрицательного числа не бывает.
Остаётся только один корень
x < 20
x ∈ ( +∞ ; 20 )
Т.к отношение площадей треугольников равно квадрату коэффициента подобия, то к=3,а SАОD /SВОС=3^2, т.е 9.
f`(x)=2x
f(0)=0
Y=1+0(x-0)=1
f(1)=1+1=2
f`(x)=2x
f(1)=2
y=2+2(x-1)=2+2x-2=2x
f(x)=-x³+3x-2
D(f)∈(-∞;∞)
f(-x)=x³-3x-2 ни четная,ни нечетная
x=0 y=-2
y=0 x=1 x=-2
(0;-2);(1;0);(-2;0)-точки пересечения с осями
f`(x)=-3x²+3=-3(x-1)(x+1)=0
x=1 U x=-1
_ + _
(-1)(1)
убыв min возр max убыв
ymin=1-3-2=-4
ymax=-1+3-2=0