![Найдите наименьшее значение функции y= на промежутке [0; 3pi/4] решить! нужно!](/tpl/images/0480/5825/fb865.jpg)
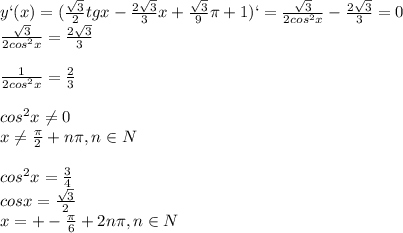
![[0;\frac{3\pi}{4}]](/tpl/images/0480/5825/1f4d5.png)
![x_{1}=\frac{\pi}{6}\in[0;\frac{3\pi}{4}]](/tpl/images/0480/5825/202f5.png)
![x_{2}=\frac{5\pi}{6}\\\\\frac{5\pi}{6}\ \textgreater \ \frac{3\pi}{4}\\\\\frac{10\pi}{6}\ \textgreater \ \frac{9\pi}{4}\\x_{2}=\frac{5\pi}{6}\notin[0;\frac{3\pi}{4}]\\](/tpl/images/0480/5825/193a8.png)
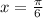 .
.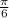 ,
, 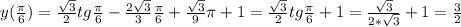
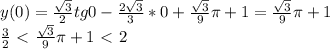
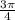 ,
,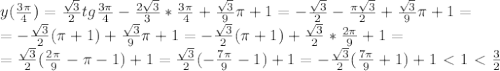 => Min!
=> Min!![Найдите наименьшее значение функции y= на промежутке [0; 3pi/4] решить! нужно!](/tpl/images/0480/5825/2ff21.jpg)
1. Разделим обе части тригонометрического неравенства на √3 и освободимся от иррациональности в знаменателе:
√3tg(3x + π/6) < 1;
tg(3x + π/6) < 1/√3;
tg(3x + π/6) < √3/3.
2. Функция тангенс имеет период π, на промежутке (-π/2, π/2) возрастает, а значение √3/3 принимает в точке π/6:
3x + π/6 ∈ (-π/2 + πk, π/6 + πk), k ∈ Z;
3x ∈ (-π/2 - π/6 + πk, π/6 - π/6 + πk), k ∈ Z;
3x ∈ (-2π/3 + πk, πk), k ∈ Z;
x ∈ (-2π/9 + πk/3, πk/3), k ∈ Z.
ответ: (-2π/9 + πk/3, πk/3), k ∈ Z.
если не правильно, напишите в коменты(
номер 3
Пусть производительность одной трубы - х, другой - у. Тогда при совместной работе, если всю работу обозначить за единицу, им потребуется 2 часа. При отдельной работе разница во времени составляет 3 часа, составим систему:
1 / (х + у) = 2,
1/х - 1/у = 3.
Из первого уравнения выразим х и подставим во второе:
1 = 2 * (х + у), 1 = 2х + 2у, 2х = 1 - 2у, х = 0,5 - у.
1 / (0,5 - у) - 1/у = 3,
у - (0,5 - у) = 3 * у * (0,5 - у),
у - 0,5 + у = -3у2 + 1,5у,
3у2 + 0,5у - 0,5 = 0,
D = b2 - 4ac
D = 0,25 - 4 * 3 * (-0,5) = 6,25.
у = (-b ± √D) / 2a
у = (-0,5 ± 2,5) / 6
у1 = -1/2, у2 = 1/3.
Решением является только положительное значение у2 = 1/3.
2) х = 0,5 - 1/3 = 1/2 - 1/3 = 3/6 - 2/6 = 1/6.
Т.е. одна труба наполняет за 1 час 1/3 цистерны, а другая 1/6. Значит одной трубе нужно 3 часа, а другой нужно 6 часов, чтобы наполнить всю цистерну при отдельной работе. Поэтому ответ задачи - 3 часа, данной трубе требуется меньшее время.
ответ: необходимо 3 часа